Tutorial Kirchhoff code

Subroutine kirchslow() below is the best tutorial Kirchhoff migration-modeling program I could devise. A nice feature of this program is that it works OK while the edge complications do not clutter it. The program copies information from data space data(it,iy) to model space modl(iz,ix) or vice versa. Notice that of these four axes, three are independent (stated by loops) and the fourth is derived by the circle-hyperbola relation 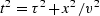$t^2=\tau^2+x^2/v^2$.Subroutine kirchslow() for adj=0 copies information from model space to data space, i.e. from the hyperbola top to its flanks. For adj=1, data summed over the hyperbola flanks is put at the hyperbola top.  

# Kirchhoff migration and diffraction.  (tutorial, slow)
#
subroutine kirchslow(   adj, add,  velhalf, t0,dt,dx, modl,nt,nx,  data)
integer ix,iy,it,iz,nz, adj, add,                          nt,nx
real x0,y0,dy,z0,dz,t,x,y,z,hs,    velhalf, t0,dt,dx, modl(nt,nx), data(nt,nx)
call adjnull(           adj, add,                     modl,nt*nx,  data,nt*nx)
x0=0.;  y0=0;  dy=dx;  z0=t0;  dz=dt; nz=nt
do ix= 1, nx {  x = x0 + dx * (ix-1)
do iy= 1, nx {  y = y0 + dy * (iy-1)
do iz= 1, nz {  z = z0 + dz * (iz-1)            # z = travel-time depth
        hs=      (x-y) / velhalf
        t = sqrt( z * z  +  hs * hs )
        it = 1.5 + (t-t0) / dt
        if( it <= nt )
                if( adj == 0 )
                        data(it,iy) = data(it,iy) + modl(iz,ix)
                else
                        modl(iz,ix) = modl(iz,ix) + data(it,iy)
        }}}
return; end

Notice how this program has the ability to create a hyperbola given an input impulse in (x,z)-space, and a circle given an input impulse in (x,t)-space.

The three loops in subroutine kirchslow() may be interchanged at will without changing the result. To emphasize this flexibility, the loops are set at the same indentation level. We tend to think of fixed values of the outer two loops and then describe what happens on the inner loop. For example, if the outer two loops are those of the model space modl(iz,ix), then for adj=1 the program sums data along the hyperbola into the ``fixed'' point of model space. When loops are reordered, we think differently and opportunities arise for speed improvements.