




Next: SETTING UP 2-D FT
Up: SETTING UP THE FAST
Previous: SETTING UP THE FAST
Subroutine simpleft() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) sets things up in a convenient manner:
The frequency range runs from minus Nyquist
up to (but not including) plus Nyquist.
Thus there is no problem with the many (but not all)
user programs that have trouble with aliased frequencies.
Subroutine ftu()
sets things up in a convenient manner:
The frequency range runs from minus Nyquist
up to (but not including) plus Nyquist.
Thus there is no problem with the many (but not all)
user programs that have trouble with aliased frequencies.
Subroutine ftu() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , however has a frequency range
from zero to double the Nyquist.
Let us therefore define a friendlier ``front end'' to ftu()
which looks more like simpleft().
, however has a frequency range
from zero to double the Nyquist.
Let us therefore define a friendlier ``front end'' to ftu()
which looks more like simpleft().
Recall that a time shift of t0 can be implemented in
the Fourier domain by multiplication by
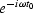 .Likewise, in the Fourier domain,
the frequency interval used by subroutine ftu()
.Likewise, in the Fourier domain,
the frequency interval used by subroutine ftu() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
namely,
,
namely, 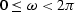 ,can be shifted to the friendlier interval
,can be shifted to the friendlier interval
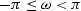 by a weighting function in the time domain.
That weighting function is
by a weighting function in the time domain.
That weighting function is 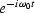 where
where 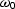 happens to be the Nyquist frequency,
i.e. alternate points on the time axis are to be multiplied by -1.
A subroutine for this purpose is fth().
happens to be the Nyquist frequency,
i.e. alternate points on the time axis are to be multiplied by -1.
A subroutine for this purpose is fth().
# FT a vector in a matrix, with first omega = - pi
#
subroutine fth( adj,sign, m1, n12, cx)
integer i, adj, m1, n12
real sign
complex cx(m1,n12)
temporary complex temp(n12)
do i= 1, n12
temp(i) = cx(1,i)
if( adj == 0) { do i= 2, n12, 2
temp(i) = -temp(i)
call ftu( sign, n12, temp)
}
else { call ftu( -sign, n12, temp)
do i= 2, n12, 2
temp(i) = -temp(i)
}
do i= 1, n12
cx(1,i) = temp(i)
return; end
To Fourier transform a 1024-point complex vector cx(1024)
and then inverse transform it, we would write
call fth( 0, 1., 1, 1024, cx)
call fth( 1, 1., 1, 1024, cx)
You might wonder about the apparent redundancy of using both
the argument adj and the argument sign.
Having two arguments instead of one allows
us to define the forward transform for a time axis
with the opposite sign as
the forward transform for a space axis.
The subroutine fth() is somewhat cluttered by
the inclusion of a
frequently needed practical feature--namely,
the facility to extract vectors from a matrix,
transform the vectors, and then restore them into the matrix.





Next: SETTING UP 2-D FT
Up: SETTING UP THE FAST
Previous: SETTING UP THE FAST
Stanford Exploration Project
12/26/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
namely,
,
namely,