Phase of a rational filter

Now let us sum up the behavior of phase of the rational filter

 

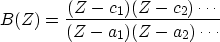$$B(Z) = {(Z - c_{1}) (Z - c_{2}) \cdots \over {(Z - a_{1}) (Z - a_{2}) \cdots}}$$ (37)

By the rules of complex-number multiplication, the phase of B(Z) is the sum of the phases in the numerator minus the sum of the phases in the denominator. Since we are discussing realizable filters, the denominator factors must all be minimum-phase, and so the denominator phase curve is a sum of periodic phase curves like the lower left of Figure 19.

The numerator factors may or may not be minimum-phase. Thus the numerator phase curve is a sum of phase curves that may resemble either type in Figure 19. If any factors augment phase by 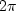$2\pi$,then the phase is not periodic, and the filter is nonminimum-phase.