Group delay as a function of the FT

We will see that the group delay of a filter P is a simple function of the Fourier transform of the filter. I have named the filter P to remind us that the theorem strictly applies only to all-pass filters, though in practice a bit of energy absorption might be OK. 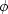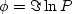The phase angle $\phi$could be computed as the arctangent of the ratio of imaginary to real parts of the Fourier transform, namely, $\phi(\omega) = \arctan [ \Im P(\omega)/ \Re P(\omega)]$.As with (12), we use $\phi =\Im \ln P$;and from (33) we get  

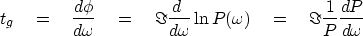$$t_g \eq \frac{d\phi}{d\omega} \eq \Im \frac{d\;}{d\omega} \ln P(\omega ) \eq \Im \frac{1}{P} \frac{dP}{d\omega}$$ (33)

which could be expressed as the Fourier dual to equation (14).