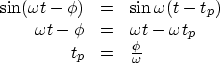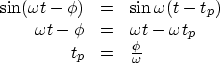Next: Group delay
Up: PHASE DELAY AND GROUP
Previous: PHASE DELAY AND GROUP
Whenever we put a sinusoid into a filter, a sinusoid
must come out.
The only things that can change between input and output are
the amplitude and the phase.
Comparing a zero crossing of the input
to a zero crossing of the output
measures the so-called
phase delay.
To quantify this, define an input, 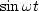 ,and an output,
,and an output, 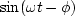 .Then the phase delay tp is found by solving
A problem with phase delay is that the phase can be ambiguous
within an additive constant of
.Then the phase delay tp is found by solving
A problem with phase delay is that the phase can be ambiguous
within an additive constant of 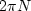 , where N is any integer.
In wave-propagation theory,
``phase velocity" is defined by
the distance divided by the phase delay.
There it is hoped that the
, where N is any integer.
In wave-propagation theory,
``phase velocity" is defined by
the distance divided by the phase delay.
There it is hoped that the 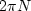 ambiguity can be
resolved by observations tending to zero frequency or physical separation.
ambiguity can be
resolved by observations tending to zero frequency or physical separation.





Next: Group delay
Up: PHASE DELAY AND GROUP
Previous: PHASE DELAY AND GROUP
Stanford Exploration Project
10/21/1998