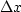)are the
same
as the physical units of the adjoint operator.
The units of an inverse operator, however, are
inverse
to the units of the original operator.
Thus it is hard to imagine that an adjoint operator
could ever be a satisfactory approximation to the inverse.
We know, however, that adjoints often are a satisfactory approximation
to an inverse,
which means then that either
(1) such operators do not have physical units, or
(2) a scaling factor in the final result is irrelevant.
With the tomographic operator,
the adjoint is quite far from the inverse
so practicioners typically work from the adjoint toward the inverse.
Some operators are arrays with different physical units for different array elements. For these operators the adjoint is unlikely to be a satisfactory approximation to the inverse since changing the units changes the adjoint. A way to bring all components to the same units is to redefine each member of data space and model space to be itself divided by its variance. Alternately, again we can abandon the idea of finding immediate utility in the adjoint of an operator and and we could progress from the adjoint toward the inverse.