




Next: Causal integration
Up: IMPEDANCE
Previous: Z - transform
Use Z-transform notation to
define a filter R(Z), its input X(Z), and its output Y(Z).
Then
| 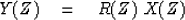 |
(20) |
The filter R(Z) is said to be
causal
if the series representation of R(Z) has no negative powers
of Z.
In other words, yt is determined from present and past
values of xt.
Additionally,
the filter R(Z) is
minimum phase
if 1/R(Z) has no negative powers of Z.
This means that xt can be determined from present and past values
of yt by straightforward polynomial division in
| 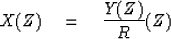 |
(21) |
Given that R(Z) is already minimum phase,
it can in addition be an
impedance function if positive energy or work is represented by
| 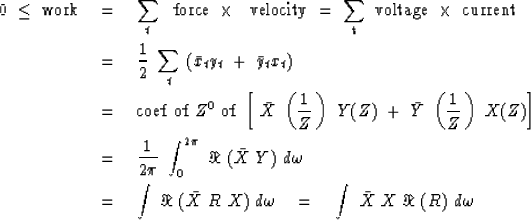 |
(22) |
| (23) |
| (24) |
| (25) |
| (26) |
Since 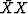 could be an impulse function located at any
could be an impulse function located at any 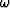 ,it follows
that
,it follows
that ![$ \Re \ [ R ( \omega ) ] \ge 0 $](img106.gif) for all real
for all real 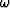 .In summary:
.In summary:
| 2|c| |
|
| 2|c| Definition of an Impedance |
|
| 2|c| |
|
| |
|
| causality |
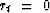 for for 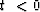 i.e. i.e.
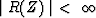 for for
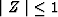 |
| |
|
| |
|
| causal inverse |
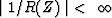 for for
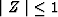 |
| |
|
| |
|
| dissipates energy |
2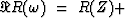 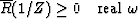 |
| |
|
Adding an impedance to its Fourier conjugate gives a real positive
function (the imaginary part of which is zero) like a power spectrum, say,
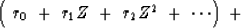
| 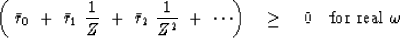 |
(27) |
| 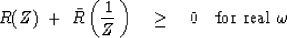 |
(28) |
which is the basis for the remarkable fact that every impedance time function
is one side of an autocorrelation function.
Impedances also arise in economic theory when X and Y are price and
sales volume.
I suppose that there the positivity of the impedance means that in the
game of buying and selling you are bound to lose!





Next: Causal integration
Up: IMPEDANCE
Previous: Z - transform
Stanford Exploration Project
10/31/1997
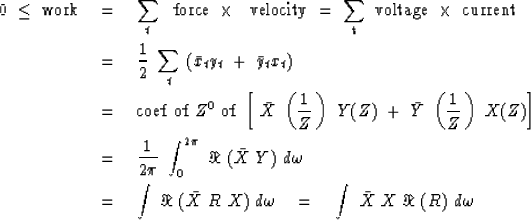
![]()