![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .)
This transformed data is downward continued
with
.)
This transformed data is downward continued
with
The phase-shift method of migration
begins with a two-dimensional Fourier transform (2D-FT) of the dataset.
(See chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .)
This transformed data is downward continued
with
.)
This transformed data is downward continued
with ![]() and subsequently evaluated
at t=0 (where the reflectors explode).
Of all migration methods,
the phase-shift method
most easily incorporates depth variation in velocity.
The phase angle and obliquity function are correctly included,
automatically.
Unlike Kirchhoff methods,
with the phase-shift method there is no danger of aliasing the operator.
(Aliasing the data, however, remains a danger.)
and subsequently evaluated
at t=0 (where the reflectors explode).
Of all migration methods,
the phase-shift method
most easily incorporates depth variation in velocity.
The phase angle and obliquity function are correctly included,
automatically.
Unlike Kirchhoff methods,
with the phase-shift method there is no danger of aliasing the operator.
(Aliasing the data, however, remains a danger.)
Equation (14) referred to upcoming waves.
However in the reflection experiment,
we also need to think about downgoing waves.
With the exploding-reflector concept of a zero-offset section,
the downgoing ray goes along the same path as the upgoing ray,
so both suffer the same delay.
The most straightforward way of converting one-way propagation
to two-way propagation is to multiply time everywhere by two.
Instead, it is customary to divide velocity everywhere by two.
Thus the Fourier transformed data values,
are downward continued to a depth ![]() by multiplying by
by multiplying by
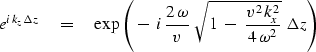 |
(15) |
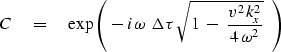 |
(16) |