Code for crosscorrelation factorization

The code below will factor the polynomial ( 2/Z + 7 + 3Z) into its two factors (3+1/Z)(2+Z) except for a scale factor which is indeterminate. Choosing to set u₀=0 leads to the interesting factorization ( 2/Z + 7 + 3Z)/6 = (1+1/(3Z)) (1+Z/2) where the scale is chosen so the coefficient of Z⁰ is 1 (a convenience when you have factored a band matrix into two parts, and plan polynomial division for back substitution). Being based on fast FT, the work space size, n, must be a power of 2. Periodicity of FT requires that one side of the crosscorrelation is at the beginning of rr(:) while the other side is at the end. A test case for ( 2/Z + 7 + 3Z) is:

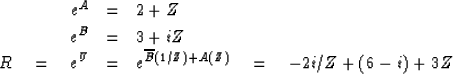
         rr( n)  =  2.        # first negative lag
         rr( 1)  =  7.        # zero lag
         rr( 2)  =  3.        # first positive lag

subroutine crossfac( n, rr, aa, bb)  # Crosscorrelation factorization.
integer i,           n               # input: rr= crosscorrelation (destroyed)
complex rr(n), aa(n), bb(n)          # output: aa and bb are minimum phase.
call fts(  1., n, rr)                         # make spectrum
rr = clog( rr )                               # log spectrum
call fts( -1., n, rr)                         # back into time domain.  
rr(1) = 0.                                    # Normalize coef of Z^0
aa = rr
bb = rr
do i= 2, n/2 {  bb(i)     = 0.                # Erase positive times.
                aa(n-i+2) = 0.                # Erase negative times.
                }                             # Halve both zero and Nyquist.
aa(1) = aa(1)/2.;    aa(1+n/2) = aa(1+n/2)/2.
bb(1) = bb(1)/2.;    bb(1+n/2) = bb(1+n/2)/2.
call fts( +1., n, aa)                         # back to frequency
call fts( +1., n, bb)
bb = cexp(  conjg( bb))                       # conjugate reverses time.
aa = cexp(         aa )
call fts( -1., n, aa)                         # minimum-phase wavelet.
call fts( -1., n, bb)                         # MP wavelet for anticausal.
return; end

To avoid any ambiguity, here is my test case for complex-valued coefficients:

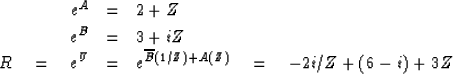$$\begin{eqnarray} e^A &=& 2+Z \\ e^B &=& 3+iZ \\ R \quad = \quad e^U &=& e^{\overline{B}(1/Z)+A(Z)} \quad = \quad-2i/Z +(6-i)+3Z\end{eqnarray}$$ (6) (7) (8)

with an output of

$$\begin{eqnarray} e^A &=& 1+Z/2 \\ e^B &=& 1+iZ/3 \end{eqnarray}$$ (9) (10)

For this case I found the errors are less than 1% when n=8. Generally, the larger the dynamic range of |R| on the unit circle the greater the need for a higher n.