

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: Balancing good data with
Up: Table of Contents
A central problem in reflection seismology is building the velocity
as a function of depth (or vertical travel time)
starting from certain measurements.
The measurements are described elsewhere (BEI for example).
They amount to measuring the integral of the velocity squared
from the surface down to the reflector.
The integral gives the RMS (root-mean-square) velocity.
Although good quality echos may arrive often,
they rarely arrive continuously for all depths.
Good information is interspersed unpredictably with poor information.
Luckily we can
also estimate
the data quality by the ``coherency'' or the
``stack energy''.
In summary, what we get from observations and preprocessing
are two functions of travel-time depth:
(1) the velocity (squared) and integrated from the surface, and
(2) a measure of the quality of the integrated velocity estimate.
Some definitions:
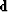
- is the data vector given to us by the preprocessing.
Its components range over the vertical
traveltime depth
 ,and its component values contain the scaled RMS velocity squared
,and its component values contain the scaled RMS velocity squared
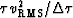 where
where
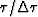 is the index on the time axis.
is the index on the time axis.
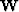
- is a diagonal matrix along which we lay the given measure
of data quality. We will use it as a weighting function.

- is the vector we seek.
Its components range over the vertical
traveltime depth
 ,and its component values contain the
local velocity (called the interval velocity) squared
,and its component values contain the
local velocity (called the interval velocity) squared
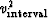 .
. 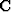
- is the matrix of causal integration, a lower triangular matrix of ones.
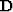
- is the matrix of causal differentiation, namely,
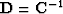 .
.
From these definitions,
under the assumption of a stratified earth with horizontal reflectors
(and no multiple reflections)
the theoretical interval velocity
enables us to define the theoretical RMS velocity by
| 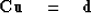 |
(1) |
Our data-fitting goal is to minimize the residual
| ![\begin{displaymath}
\bold 0
\quad\approx\quad
\bold W
\left[
\bold C\bold u
-
\bold d
\right]\end{displaymath}](img12.gif) |
(2) |
To find the interval velocity
where there is no data (where the stack power vanishes)
we have the ``model damping'' goal to minimize
the wiggliness  of the (squared) interval velocity
of the (squared) interval velocity  .
.
| 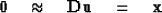 |
(3) |
We ``precondition'' these two goals
by changing the optimization variable from
interval velocity squared
 to its wiggliness
to its wiggliness  .Substituting
.Substituting 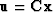 gives the two goals
expressed as a function of wiggliness
gives the two goals
expressed as a function of wiggliness  .
.
| ![\begin{eqnarray}
\bold 0
&\approx&
\bold W
\left[
\bold C^2\bold x
-
\bold d
\right]
\\ \bold 0
&\approx&
\epsilon \; \bold x\end{eqnarray}](img16.gif) |
(4) |
| (5) |


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: Balancing good data with
Up: Table of Contents
Stanford Exploration Project
2/5/1998
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![]() of the (squared) interval velocity
of the (squared) interval velocity ![]() .
.
![]() to its wiggliness
to its wiggliness ![]() .Substituting
.Substituting ![]() gives the two goals
expressed as a function of wiggliness
gives the two goals
expressed as a function of wiggliness ![]() .
.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)