




Next: ROUGHENERS AND SMOOTHERS
Up: Claerbout: Preconditioning and scalingPreconditioning
Previous: ROW NORMALIZATION, POSITIVE OPERATORS
Sometimes an operator 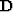 does not contain all positive numbers,
but we can easily form another operator
which, element by element,
has the absolute values of the elements of
does not contain all positive numbers,
but we can easily form another operator
which, element by element,
has the absolute values of the elements of 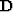 .An example of this arises with estimation
of prediction-error filters where the matrix
.An example of this arises with estimation
of prediction-error filters where the matrix 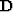 ,contains raw seismic data.
It is easy enough to replace each seismic data value
by its absolute value.
I'll write this as
,contains raw seismic data.
It is easy enough to replace each seismic data value
by its absolute value.
I'll write this as 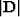 where it is understood that the absolute values are applied
to each component in the matrix
where it is understood that the absolute values are applied
to each component in the matrix 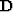 .In reality we would not have the matrix itself,
but we would make a filter of all ones,
and convolve it with the seismic magnitudes;
I'll write this as
.In reality we would not have the matrix itself,
but we would make a filter of all ones,
and convolve it with the seismic magnitudes;
I'll write this as
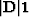 .Obviously this absolute-valued data could be smoothed;
it could have a tiny threshold
.Obviously this absolute-valued data could be smoothed;
it could have a tiny threshold  added;
and it could then be inverted and used as a weighting function.
added;
and it could then be inverted and used as a weighting function.
A use of this weighting function is when we are
estimating a prediction-error filter from noisy data.
We choose a scaling factor for each fitting equation equal to the
inverse to the sum of the absolute values of the elements on the row.
Thus, where there are spikes in the data,
we have scaled each defective fitting equation
by the inverse of the spike (the spike plus other positive values).
Notice that we still have a linear problem.
Since we are not scaling by the inverse residual,
the solution is still easy weighted least squares;
we don't need complicated robust L1 solvers.





Next: ROUGHENERS AND SMOOTHERS
Up: Claerbout: Preconditioning and scalingPreconditioning
Previous: ROW NORMALIZATION, POSITIVE OPERATORS
Stanford Exploration Project
11/11/1997