

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Evaluating the Stolt stretch parameter
Sergey Fomel
sergey@sep.stanford.edu
ABSTRACT
The Stolt migration extension to a varying velocity case (Stolt
stretch) implies
describing a vertical heterogeneity by a constant parameter
(W). This paper
exploits the connection between modified dispersion relations and traveltime
approximations to derive an
explicit expression for W. The expression provides theoretically the
highest possible accuracy
within
the Stolt
stretch framework. Applications considered include optimal partitioning
of the velocity distribution for the cascaded migrations and extension
of the Stolt stretch method to transversally isotropic models.
|
Stolt migration is regarded as the fastest post-stack migration method of
all the known algorithms. A known price for that speed is the constant
velocity assumption. The time-stretching trick proposed in Stolt's
classic paper provides an approximate
extension of
the method to a variable velocity case.
Stolt stretch implicitly transforms reflection traveltime curves to fit
an approximate constant velocity pattern
(, , ). In
other words, the wave equation with variable velocity is transformed
by a particular stretch of the time axis to an approximate
differential equation
with
constant coefficients. The two constant coefficients are
an arbitrarily chosen frame
velocity and a specific nondimensional parameter (W in Stolt's
original notation). In the constant velocity case W is equal to 1, and the
transformed equation coincides with the exact constant velocity wave equation. In
variable velocity media, W is generally assumed to lie between and
1. As shown
by Beasley et al. , the cascaded
f-k migration approach can move the value of W for each
migration in a cascade closer to 1, thus increasing the accuracy of
the Stolt
stretch approximation.
The W factor was defined by
Stolt as an approximate average
of a complicated function. Stolt's definition
cannot be used directly for
computation because it includes a combined dependence on
both time and space coordinates. Therefore,
in practice, the estimation of this factor is always replaced by
a heuristic guess. That's why Levin
called the W parameter ``infamous'' (joking, of course), and Beasley
et al. called it it ``esoteric.''
This paper develops a method to evaluate the Stolt
stretch parameter explicitly. The main idea is to constrain
the parameter by fitting the exact and
approximated
traveltime functions.
In the case of isotropic interpretation, the W parameter is
connected to the ``parameter of heterogeneity''
(, , ). In the case of
anisotropic (transversally isotropic) interpretation, it can be related
to the ``parameter of anellipticity'' (, ).
STOLT STRETCH THEORY
In order to simplify the references, I will begin with the textbook
definitions of
the Stolt migration
method. The reader familiar with Stolt stretch theory can skip this
section and go on to
a new piece of theory in the next one.
Post-stack seismic migration is theoretically a two-stage process
consisting of wavefield downward continuation in depth z based on
the wave equation
| 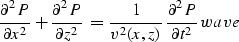 |
(1) |
and the imaging condition t=0 (here the velocity v is twice as
small as
the actual wave velocity).
Stolt time migration performs both stages in one step, applying the
frequency-domain
operator
| 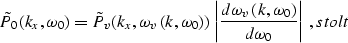 |
(2) |
where
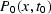 stands for the initial zero-offset (stacked)
seismic
section defined on the surface z=0,
stands for the initial zero-offset (stacked)
seismic
section defined on the surface z=0,
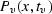 is the time-migrated section, and tv is
the vertical traveltime
is the time-migrated section, and tv is
the vertical traveltime
| 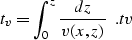 |
(3) |
The function
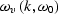 in stolt corresponds to the dispersion
relation of
the wave equation wave and in the constant velocity case has the explicit
expression
in stolt corresponds to the dispersion
relation of
the wave equation wave and in the constant velocity case has the explicit
expression
| 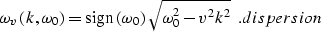 |
(4) |
The choice of the sign in dispersion is essential to distinguish
between
upgoing and downgoing waves. It is the upgoing part of the wave field
that is used in migration.
For the case of a varying velocity Stolt
suggested the following change
of the time variable (referred to in the literature as Stolt stretch):
| 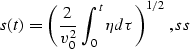 |
(5) |
where v0 is an arbitrarily chosen constant velocity, and 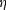 is a
function defined by the parametric expressions
is a
function defined by the parametric expressions
| 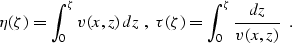 |
(6) |
With the stretch ss, seismic time migration can be
related to the transformed wave equation
| 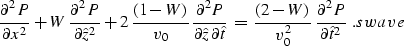 |
(7) |
Here 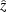 and
and 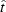 are the transformed depth and time coordinates that
possess
the following property: if
are the transformed depth and time coordinates that
possess
the following property: if 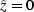 ,
, 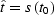 , and if
, and if
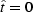 ,
, 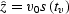 . W is a varying
coefficient defined as
. W is a varying
coefficient defined as
| 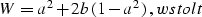 |
(8) |
where
Stolt's idea was to replace the slowly varying parameter W with its average
value.
Thus equation swave is approximated by an equation with constant
coefficients, which has the dispersion relation
| 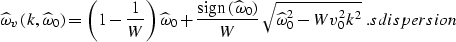 |
(9) |
Stolt's approximate method for migration in heterogeneous media consists of the
following steps:
- 1.
- stretching the time variable according to ss,
- 2.
- interpolating the stretched time to a regular grid,
- 3.
- double Fourier transform,
- 4.
- f-k time migration by operator stolt with the dispersion
relation
sdispersion,
- 5.
- inverse Fourier transform,
- 6.
- inverse stretching (shrinking) the vertical time variable on the migrated
section.
The value of W must be chosen prior to migration. According to
Stolt's original definition wstolt,
the depth variable z gradually changes in the migration process from
zero to 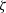 , causing the coefficient
b in wstolt to change monotonically from 0 to 1. If the velocity v
monotonically increases with depth, then
, causing the coefficient
b in wstolt to change monotonically from 0 to 1. If the velocity v
monotonically increases with depth, then
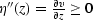 , and the average value of b is
, and the average value of b is
| 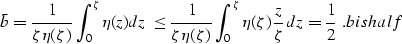 |
(10) |
As follows from wstolt and bishalf, in the case of monotonically
increasing
velocity, the average value of W has to be less than 1 (W equals 1 in a
constant
velocity case). Analogously, in the case of a monotonically decreasing
velocity, W is always greater than 1.
In practice, W is included in migration routines as a
user-defined
parameter, and its value is usually chosen to be somewhere in the
range of 1/2 to 1.
In this
paper I will describe a straightforward way to determine the most
appropriate value of W for a given velocity distribution.
A useful tool for that purpose is Stewart Levin's formula for the
traveltime curve. Levin applied the
stationary phase technique
to the dispersion relation sdispersion to obtain an explicit formula for
the
summation curve of the integral migration operator analogous to the
Stolt stretch
migration. The formula evaluates the summation path in the stretched
coordinate system, as follows:
| 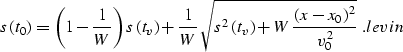 |
(11) |
Here x0 is the midpoint location on a zero-offset seismic section,
and x is the
space coordinate on the migrated section.
Formula levin shows that, with the stretch of the time coordinate, the
summation curve has the
shape of a hyperbola with the apex at 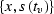 and
the center (the intersection of the asymptotes) at
and
the center (the intersection of the asymptotes) at
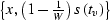 . In the case
of homogeneous media, W=1,
. In the case
of homogeneous media, W=1, 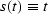 , and levin reduces to the
well-known
hyperbolic diffraction traveltime curve. It is interesting to note
that inverting formula levin for
, and levin reduces to the
well-known
hyperbolic diffraction traveltime curve. It is interesting to note
that inverting formula levin for 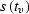 determines
the impulse response of the migration operator, which can be
interpreted as
the wavefront from a point source in the
determines
the impulse response of the migration operator, which can be
interpreted as
the wavefront from a point source in the
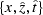 domain of equation
swave:
domain of equation
swave:
| 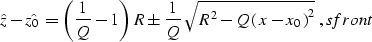 |
(12) |
where 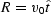 , and Q=2-W.
According to equation sfront, wavefronts from a point source in
the stretched
coordinates
for W<2 have an elliptic shape, with the center of the ellipse
at
, and Q=2-W.
According to equation sfront, wavefronts from a point source in
the stretched
coordinates
for W<2 have an elliptic shape, with the center of the ellipse
at
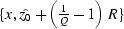 and the semi-axes
and the semi-axes
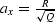 and
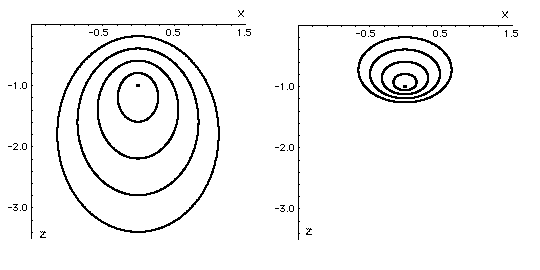
and 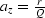 . The ellipses stretch
differently for W<1 and W>1 (Figure stofro). In the upper part
that corresponds to the upgoing waves, they look nearly spherical, since
the radius of the front curvature at the top apex equals the distance from the
source.
stofro
. The ellipses stretch
differently for W<1 and W>1 (Figure stofro). In the upper part
that corresponds to the upgoing waves, they look nearly spherical, since
the radius of the front curvature at the top apex equals the distance from the
source.
stofro
Figure 1 Wavefronts from a point
source in the stretched coordinate system. Left: velocity decreases with depth
(W=1.5). Right: velocity increases with depth (W=0.5).

EVALUATING THE W PARAMETER AND STOLT STRETCH ACCURACY
Formula levin belongs to the three-parameter class of traveltime
approximations. The key result of this paper uses
a remarkable formal similarity between levin and
Malovichko's
approximation for the reflection traveltime curve in vertically inhomogeneous
media
(, , ) defined by
| 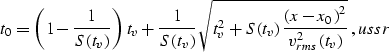 |
(13) |
where vrms stands for the effective (root mean square) velocity along the
vertical
ray
| 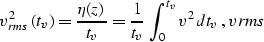 |
(14) |
and S is the parameter of heterogeneity:
| 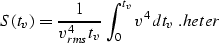 |
(15) |
In terms of the S parameter, the variance of the squared velocity
distribution along the vertical ray
is
| 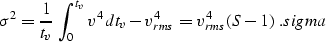 |
(16) |
As follows from equality sigma, 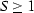 for any type of
velocity distribution
(S
equals 1 in a constant velocity case). For most of the distributions occurring
in
practice, S ranges between 1 and 2.
for any type of
velocity distribution
(S
equals 1 in a constant velocity case). For most of the distributions occurring
in
practice, S ranges between 1 and 2.
Malovichko's formula ussr is known as the
most accurate three-parameter approximation of the NMO curve in vertically
inhomogeneous media.
Since reflection from a horizontal reflector in that class of media is
kinematically
equivalent to diffraction from a point, formula ussr
can be similarly regarded as an approximation of the summation path of the
post-stack Kirchhoff-type migration operator. In this case, it has the same
meaning as formula levin. An important difference between the
two formulae is the fact
that
equation ussr is written in the initial coordinate system and includes coefficients
varying with depth, while equation levin applies the transformed coordinate system
and
constant coefficients. Using this fact, the rest of this section
compares the accuracy of the approximations and relates Stolt's W factor to
Malovichko's parameter of heterogeneity.
Equations levin and ussr both approximate the
traveltime
curve in the neighborhood of the vertical ray. Therefore,
to compare their accuracy, it is
appropriate to consider series expansion of the diffraction traveltime in the
vicinity of the vertical ray![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
:
| 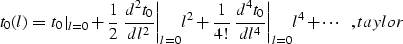 |
(17) |
where l=x-x0.
Expansion taylor contains only even powers of l because of
the obvious symmetry of t0 as a function of l.
The special choice of parameters tv, vrms, and S allows
Malovichko's formula
ussr to provide correct values for the first
three terms of expansion taylor:
| 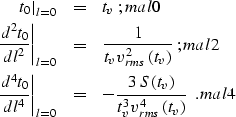 |
(18) |
| (19) |
| (20) |
Considering Levin's formula levin as an implicit definition of the function
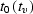 , we can iteratively differentiate it following the
rules of calculus:
, we can iteratively differentiate it following the
rules of calculus:
| 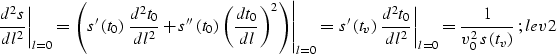 |
(21) |
| 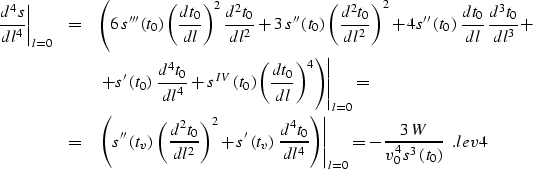 |
|
| |
| (22) |
Substituting the definition of Stolt stretch transform ss into lev2
produces an equality similar to mal2, which means that approximation
levin is theoretically accurate in depth-varying velocity media up to the
second term in taylor. It is this remarkable property that
proves the validity of the Stolt stretch method
(, ). Formula levin will be
accurate
up to the third term if the value of the fourth-order traveltime derivative in
lev4 coincides with mal4. Substituting equation mal4 into
lev4
transforms the latter to the form
| 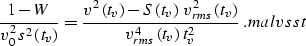 |
(23) |
It is now easy to derive from equation malvsst the desired
explicit expression for the
Stolt stretch
parameter W, as follows:
| 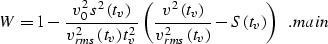 |
(24) |
Expression main is derived so as to provide
the best possible value of W for a given depth (vertical time tv). To get a
constant value for a range of depths one should take an average of the right hand
side of
main in that range.
The error associated with Stolt stretch can be approximately estimated
from
taylor as the difference between the fourth-order terms:
| 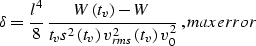 |
(25) |
where 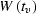 is the right-hand side of main, and W is the
constant value of W chosen for Stolt migration.
is the right-hand side of main, and W is the
constant value of W chosen for Stolt migration.
To estimate the best possible
accuracy that the Stolt stretch method can achieve, we must take into
account
the sixth-order
term in taylor related to the sixth-order derivative of the
traveltime curve. For the true traveltime curve,
the expression for the sixth-order derivative in the vicinity of the
vertical ray
is
known from the literature (, ) to be
| 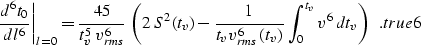 |
(26) |
First, let us estimate the error of Malovichko's approximation ussr.
Differentiating ussr six times and setting the offset l to zero yields
| 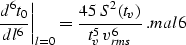 |
(27) |
The estimated error is proportional to the difference between mal6 and
true6:
| ![\begin{displaymath}
\delta_M={{l^6} \over {6!}}\,\left[
{{45} \over {t_v^5\, v_{...
...dt_v-S^2\left(t_v\right)
\right)\right]\;.
\EQNLABEL{malerror} \end{displaymath}](img54.gif) |
(28) |
It is interesting to note that replacing the parameter of heterogeneity S by its definition
heter changes the expression in the round brackets to the following
form:
| 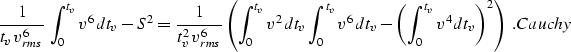 |
(29) |
According to the Schwarz inequality from calculus (
also known as the Cauchy-Bunyakovski inequality), the value
of expression Cauchy can never
be less
than zero; hence 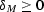 for any velocity distribution. This
conclusion indicates
that Malovichko's approximation tends to increase the traveltime at large
offsets beyond its true value.
for any velocity distribution. This
conclusion indicates
that Malovichko's approximation tends to increase the traveltime at large
offsets beyond its true value.
Differentiating lev4 twice and eliminating terms that vanish at l=0 produces
| 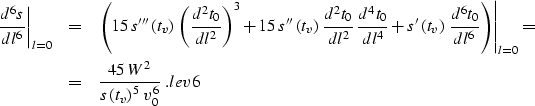 |
|
| (30) |
Evaluating the sixth-order traveltime derivative from lev6 and
subtracting
true6, we get a somewhat lengthy but explicit expression for the error
associated
with Stolt stretch approximation in the case of the best possible
choice of W:
| ![\begin{displaymath}
+ {l^6 \over 6!}\,\left[
{{45\, \left( 1-W \right) } \over
...
..._v^4\,v_{rms}^8\left(t_v\right)}}
\right]\;.
\EQNLABEL{leverr} \end{displaymath}](img59.gif) |
(31) |
ISOTROPIC HETEROGENEITY VERSUS ANELLIPTIC ANISOTROPY
A controversial issue associated with the topic of this paper is
whether the non-hyperbolicity of the traveltime curves is caused mainly by
heterogeneity or by anisotropy. To find a connection
between the two
different descriptions of media, we can consider an alternative
three-parameter traveltime approximation (the anelliptic
anisotropic moveout formula), proposed by Muir and Dellinger
:
| 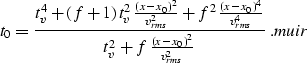 |
(32) |
Here f is the parameter of anellipticity.
Differentiating muir four times, setting l=x-x0 to zero, and equating
the result with mal4 results in the following formal
relationship between f
and Malovichko's parameter of heterogeneity:
| 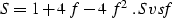 |
(33) |
Equation Svsf clearly demonstrates the uncertainty between the
anisotropic and heterogeneous isotropic interpretations. Both of them
can explain the cause of the nonhyperbolicity of traveltime curves. An
important difference is that the parameter of heterogeneity is
uniquely determined by the velocity distribution according to
heter, while the f parameter is assumed to be an independent
functional. The definition heter, applied in combination with
main, is suitable for calculating the Stolt stretch factor in an
isotropic model for a given velocity function. If the correction
parameter is measured experimentally by a non-hyperbolic velocity analysis
in
the form of either equation ussr or equation muir, it accumulates both heterogeneous
and
anisotropic factors and can be used for an
explicit determination of W in main independently of the
preferred explanation. In the case of the
anisotropic moveout velocity analysis, we merely need
to substitute the connection formula
Svsf into main to find W. An alternative approach to Stolt-type
migration in
transversally isotropic media was proposed recently by Ecker
and Muir . However, Stolt stretch migration
is superior to that method in its ability to cope with varying rms velocities.
EXAMPLES
A simple analytic example of isotropic heterogeneity is the case of a
constant velocity gradient. In this
case the velocity distribution can be described by the linear function
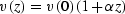 . Stolt stretch transform is found
from ss as
. Stolt stretch transform is found
from ss as
| 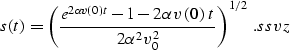 |
(34) |
Let  be the logarithm of the velocity change v(z)/v(0). Then an
explicit expression for W factor follows from main:
be the logarithm of the velocity change v(z)/v(0). Then an
explicit expression for W factor follows from main:
| 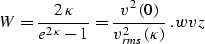 |
(35) |
For
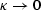 (a small depth or a small velocity gradient),
(a small depth or a small velocity gradient), 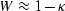 . For
. For
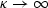 (a large positive change of velocity) W
monotonically approaches zero. Formula wvz can be a useful rule
of thumb for a rough
estimation of W.
(a large positive change of velocity) W
monotonically approaches zero. Formula wvz can be a useful rule
of thumb for a rough
estimation of W.
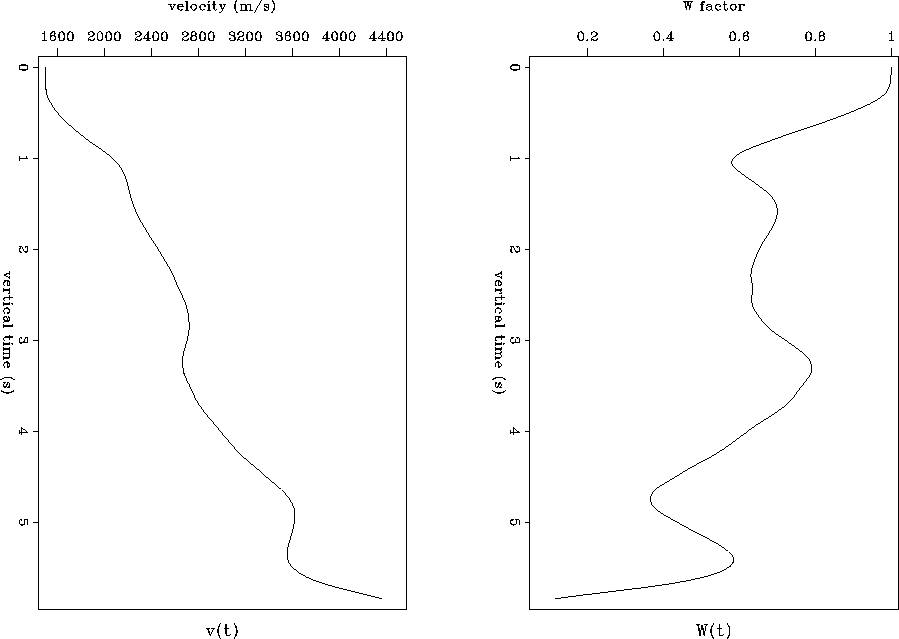
Numerical example of the Stolt stretch parameter computation is
illustrated in Figures stovwt and stocvw. The left side of
Figure stovwt shows a smoothed
interval velocity curve from the Gulf of Mexico. The corresponding
optimal values of the W factor as a function of vertical time (in the
isotropic model) are shown on the
right. Though the velocity function is smooth, substantial changes in W
occur, making its mean value for the times 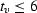 sec equal to
0.631.
sec equal to
0.631.
The theory of cascaded migrations
(, ) proves that Stolt-type f-k
migration for a nonuniform velocity 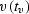 can be
performed as a cascaded process consisting of
migrations with the smaller velocities
can be
performed as a cascaded process consisting of
migrations with the smaller velocities
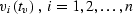 , such that
, such that
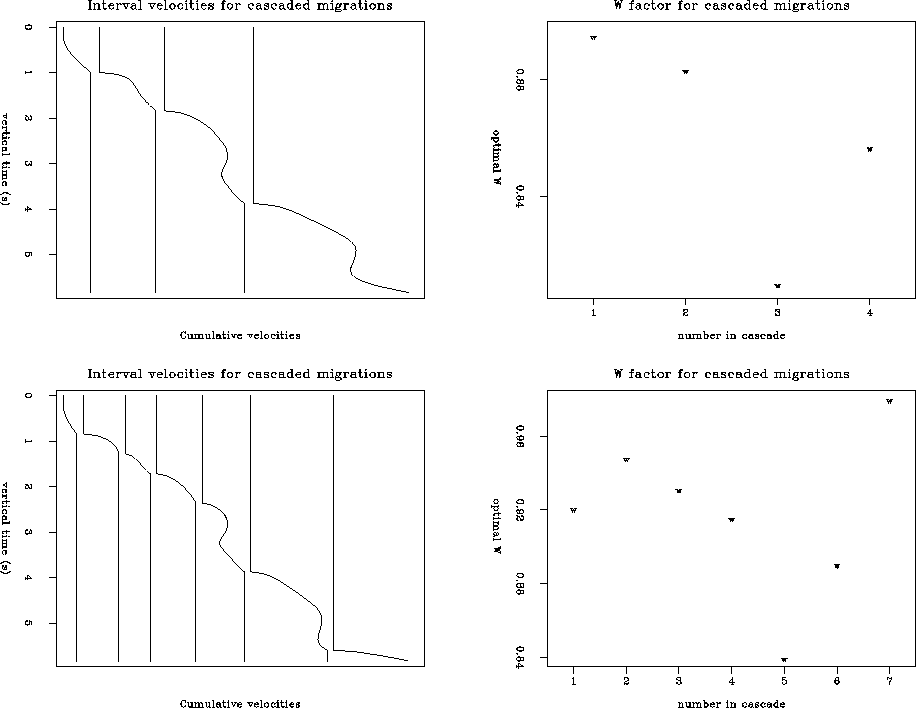
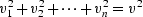 . As shown by Larner and Beasley
, it is important to partition the
velocity so that for each particular tv all the
velocities in the cascade, except maybe the last one, are constant. The
advantage of the cascaded f-k migration method is based on the
fact that each small velocity vi describes a more homogeneous medium
than the initial
. As shown by Larner and Beasley
, it is important to partition the
velocity so that for each particular tv all the
velocities in the cascade, except maybe the last one, are constant. The
advantage of the cascaded f-k migration method is based on the
fact that each small velocity vi describes a more homogeneous medium
than the initial 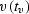 function. Therefore, the W factor
for each migration in a cascade is closer to 1, and the Stolt
stretch approximation is more accurate. This fact is illustrated in Figure
stocvw, which shows an optimal partitioning of the velocity and
the corresponding values of the W factor. In accordance
with the empirical conclusions of Beasley et al. ,
a cascade of only four migrations was sufficient to increase the value of W
to more than 0.8. With a further
increase of the number of cascaded migrations, the
method
becomes as accurate with respect to vertical velocity variations as phase-shift
migration. Theoretically, this limit corresponds to the velocity continuation
concept (). Note that the theory of
cascaded f-k migration is strictly valid for isotropic models. The anisotropic interpretation
does not support it, since the intrinsic
anisotropy
factor is not supposed to change with the velocity partitioning.
function. Therefore, the W factor
for each migration in a cascade is closer to 1, and the Stolt
stretch approximation is more accurate. This fact is illustrated in Figure
stocvw, which shows an optimal partitioning of the velocity and
the corresponding values of the W factor. In accordance
with the empirical conclusions of Beasley et al. ,
a cascade of only four migrations was sufficient to increase the value of W
to more than 0.8. With a further
increase of the number of cascaded migrations, the
method
becomes as accurate with respect to vertical velocity variations as phase-shift
migration. Theoretically, this limit corresponds to the velocity continuation
concept (). Note that the theory of
cascaded f-k migration is strictly valid for isotropic models. The anisotropic interpretation
does not support it, since the intrinsic
anisotropy
factor is not supposed to change with the velocity partitioning.
stovwt
Figure 2 Smoothed interval
velocity distribution from the Gulf of Mexico (left) and the corresponding
W factor as a function of vertical time (right). The mean value of W
is 0.631.




 stocvw
stocvw
Figure 3 Left: Optimal
partitioning of the velocity function for the
method of cascaded migrations. Right: corresponding mean values of
W. Top: four cascaded migrations. Bottom: seven cascaded migrations.





The main result of this paper is an analytic explicit expression
main that
allows us to choose the most appropriate value for the Stolt stretch
factor. Possible applications include the optimal
design
of interval velocities partitioning for the method of cascaded f-k
migrations and extension of the Stolt stretch method to a
transversally isotropic model.
Nowadays the topic of this paper seems to be out of fashion. When everyone is
interested in prestack depth migration in the time-space domain, it
is difficult to attract any attention to post-stack
time migration in the frequency domain. Nevertheless,
I believe the art of
approximation demonstrated by Robert Stolt in his famous paper to be a good
example
to follow when working on many different problems, which was the main
reason for
this research.
[SEP,MISC,GEOTLE,paper,SEGCON]


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
5/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
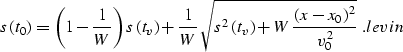
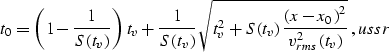
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
:
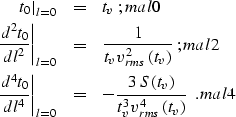
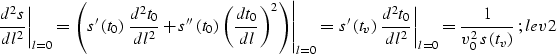
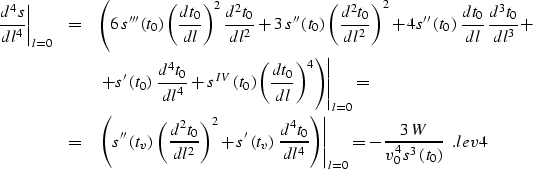
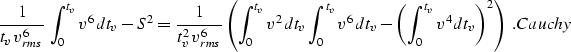
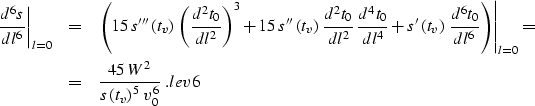
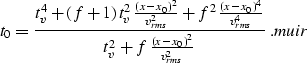
![]() . Stolt stretch transform is found
from ss as
. Stolt stretch transform is found
from ss as
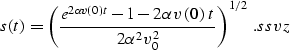
![]() sec equal to
0.631.
sec equal to
0.631.
![]() can be
performed as a cascaded process consisting of
migrations with the smaller velocities
can be
performed as a cascaded process consisting of
migrations with the smaller velocities
![]() , such that
, such that
![]() . As shown by Larner and Beasley
, it is important to partition the
velocity so that for each particular tv all the
velocities in the cascade, except maybe the last one, are constant. The
advantage of the cascaded f-k migration method is based on the
fact that each small velocity vi describes a more homogeneous medium
than the initial
. As shown by Larner and Beasley
, it is important to partition the
velocity so that for each particular tv all the
velocities in the cascade, except maybe the last one, are constant. The
advantage of the cascaded f-k migration method is based on the
fact that each small velocity vi describes a more homogeneous medium
than the initial ![]() function. Therefore, the W factor
for each migration in a cascade is closer to 1, and the Stolt
stretch approximation is more accurate. This fact is illustrated in Figure
stocvw, which shows an optimal partitioning of the velocity and
the corresponding values of the W factor. In accordance
with the empirical conclusions of Beasley et al. ,
a cascade of only four migrations was sufficient to increase the value of W
to more than 0.8. With a further
increase of the number of cascaded migrations, the
method
becomes as accurate with respect to vertical velocity variations as phase-shift
migration. Theoretically, this limit corresponds to the velocity continuation
concept (). Note that the theory of
cascaded f-k migration is strictly valid for isotropic models. The anisotropic interpretation
does not support it, since the intrinsic
anisotropy
factor is not supposed to change with the velocity partitioning.
function. Therefore, the W factor
for each migration in a cascade is closer to 1, and the Stolt
stretch approximation is more accurate. This fact is illustrated in Figure
stocvw, which shows an optimal partitioning of the velocity and
the corresponding values of the W factor. In accordance
with the empirical conclusions of Beasley et al. ,
a cascade of only four migrations was sufficient to increase the value of W
to more than 0.8. With a further
increase of the number of cascaded migrations, the
method
becomes as accurate with respect to vertical velocity variations as phase-shift
migration. Theoretically, this limit corresponds to the velocity continuation
concept (). Note that the theory of
cascaded f-k migration is strictly valid for isotropic models. The anisotropic interpretation
does not support it, since the intrinsic
anisotropy
factor is not supposed to change with the velocity partitioning.
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)