

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Amplitude preserving AMO from true amplitude DMO and inverse DMO
Nizar Chemingui and Biondo Biondi
nizar@sep.stanford.edu, biondo@sep.stanford.edu
ABSTRACT
Starting from the definition of Azimuth Moveout (AMO) as the cascade
of DMO and inverse DMO at different offsets and azimuths, we derive
an amplitude-preserving function for the AMO operator.
This amplitude function is based on the FK definition of DMO
and the definition of its true inverse. Similar to Liner's formalism
of a true inverse for Hale's DMO,
we derive an asymptotically true inverse for Black/Zhang's DMO
and Bleinstein's Born DMO.
A numerical test is given that
compares amplitude preservation using kinematically equivalent
DMO operators cascaded
with their true inverses.
We define amplitude-preserved processing as the preservation of the
offset-dependent reflectivity after AMO transformation, where the
reflectivity is considered to be proportional to the peak amplitude
of each event.
We found that an AMO operator defined using
Zhang's DMO cascaded with its true inverse best reconstructs data amplitudes
after transformation to a new offset and azimuth.
The new amplitude function represents
an amplitude-preserving azimuth moveout.
|
Previously, Biondi and Chemingui introduced a
partial-migration operator named Azimuth-Offset
Moveout (AMO) that rotates the data azimuth and
changes the data absolute offset.
The AMO operator can be defined as the cascade of an imaging operator
that acts on data with a given offset and azimuth, followed
by a forward modeling operator that reconstructs the data
at a different offset and azimuth.
In the context of amplitude preserving processing, we need to derive
a true amplitude function for AMO so that amplitude variations as a
function of offset and azimuth are not distorted by this operation.
Because we derived AMO from DMO, AMO potentially has
amplitude effects similar to those of DMO. Starting from the general definition
of DMO in the FK domain (, , ) and the
definition of a general inverse DMO
(, ), we
derived inverses for Zhang's DMO and for Bleistein's Born DMO. Our
derivation of true inverses is similar to that
of Liner
for an amplitude-preserved inverse for Hale's DMO. The
approach is based on a general formalism for inverting integral solutions
(, ) that we use to derive a solution
for an integral inverse DMO that is asymptotically valid.
Our motivation for this approach is to compare our inverses
to an inverse DMO formula
of Ronen's and Liner's
. A best amplitude-preserving DMO cascaded with
its true amplitude inverse is then selected to define an amplitude
preserving AMO. We used this AMO operator in an
amplitude-preserved processing sequence consisting of spherical divergence,
normal-moveout (NMO), azimuth moveout (AMO) and inverse NMO.
We conducted numerical experiments by transforming data from a given
azimuth and absolute offset to a new azimuth and offset using different
AMO operators defined from kinematically equivalent DMO's and inverse
DMO's. We tested for amplitude preservation by studying the offset-dependent
reflectivity through peak amplitudes along a dipping event
after the AMO transformation. According to
most interpreters, ``true-amplitude''
means that each event's peak is proportional to the reflection
coefficient.
In the next section we will briefly review the definition of the AMO
operator, describe the general solution for an
asymptotically valid inverse DMO () and then derive a
true inverse for Zhang's DMO and Bleistein's
Born DMO .
AZIMUTH MOVEOUT OPERATOR
We define AMO as an operator that transforms 3-D prestack data
with a given offset and azimuth to equivalent data
with different offsets and azimuths ().
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
a graphical representation of this offset transformation;
the input data with offset
shows
a graphical representation of this offset transformation;
the input data with offset
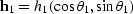 is transformed into data with offset
is transformed into data with offset
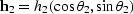 .AMO is not a single-trace to single-trace transformation,
but moves events across midpoints according to their dip.
Therefore, AMO is a partial-migration operator.
.AMO is not a single-trace to single-trace transformation,
but moves events across midpoints according to their dip.
Therefore, AMO is a partial-migration operator.
The AMO operator is defined in the the zero-offset frequency 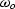 and
midpoint wavenumber
and
midpoint wavenumber 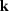 as
as
| 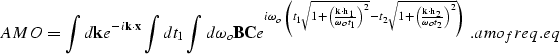 |
(1) |
The traveltimes t1 and t2 are, respectively, the
traveltime of the input data after NMO, and the traveltime of the
results before application of inverse NMO. 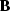 and
and 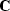 are the
Jacobians in the FK definition of the DMO operator and the definition of
its inverse DMO-1.
sketchwidth=4.2inNR
Map view of offset and azimuth of AMO input and output traces.
are the
Jacobians in the FK definition of the DMO operator and the definition of
its inverse DMO-1.
sketchwidth=4.2inNR
Map view of offset and azimuth of AMO input and output traces.
Since 3-D prestack data are often irregularly sampled,
it is necessary to define AMO as
an integral operator in the time-space domain.
A stationary-phase approximation of amo_freq.eq yields a
time-space representation
of the AMO operator where the equation for the kinematics of the
impulse response is ()
| 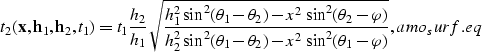 |
(2) |
while the amplitudes are given by
| 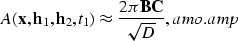 |
(3) |
where 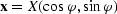 is the output location
vector in
midpoint coordinates and D is the determinant of a Hessian matrix.
For given input half-offset and time (
is the output location
vector in
midpoint coordinates and D is the determinant of a Hessian matrix.
For given input half-offset and time (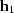 , t1) and
output half-offset
, t1) and
output half-offset 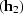 ,equations amo_surf.eq and amo.amp
define a surface in the time-midpoint space.
The surface is a skewed saddle; its shape and spatial extent
are controlled by the medium velocity, the absolute offsets
and by the azimuth rotation, i.e.,
the differences in azimuths between the input and the output data
(, ).
The Jacobians
,equations amo_surf.eq and amo.amp
define a surface in the time-midpoint space.
The surface is a skewed saddle; its shape and spatial extent
are controlled by the medium velocity, the absolute offsets
and by the azimuth rotation, i.e.,
the differences in azimuths between the input and the output data
(, ).
The Jacobians 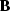 and
and 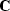 and the determinant
and the determinant  in
equation amo.amp are actually
evaluated at the stationary point of the phase function in the integral
kernel of amo_freq.eq. We present an explicit formula for them
for different cases of DMO's in Appendix A.
in
equation amo.amp are actually
evaluated at the stationary point of the phase function in the integral
kernel of amo_freq.eq. We present an explicit formula for them
for different cases of DMO's in Appendix A.
The amplitude behavior of AMO is completely controlled by the amplitude
functions of the DMO operator and its inverse. An amplitude correct
AMO should follow from a true amplitude DMO and its amplitude-preserving
inverse. Liner and Cohen argued that an adjoint
DMO operator
is a poor representation
of an inverse DMO. They showed that for the case of Hale DMO, the application
of DMO followed by its adjoint inverse can result in a serious amplitude
degradation. They proposed instead a solution for an asymptotically
valid inverse DMO and derived a true inverse for Hale's DMO. In the next
section we outline their solution and apply it in order
GENERAL FORMALISM FOR INVERSE DMO
DMO is a method of transformation of finite-offset data
to zero-offset data. Let the normal moveout corrected input data be
denoted 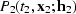 and the zero-offset desired
output denoted
and the zero-offset desired
output denoted 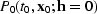 . Assume known relationships between
the coordinates of the general form
. Assume known relationships between
the coordinates of the general form
| 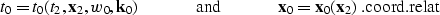 |
(4) |
The DMO operator can be
defined in the zero-offset frequency 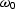 and midpoint
wavenumber
and midpoint
wavenumber 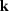 as ()
as ()
| ![\begin{eqnarray}
P_0(\omega_{0},{\bf k}_0;{\bf h}=0)&=&\int d{\bf x}_2 \frac {d{...
...bf x}_2)\right]} P_2(t_2,{\bf x}_2;{\bf h}_2), \
\EQNLABEL{dmo.eq}\end{eqnarray}](img18.gif) |
(5) |
| (6) |
whereas its inverse can be defined as:
| ![\begin{displaymath}
P_2(t_2,{\bf x}_2;{\bf h}_2)=\int d{\bf k}_0 \int d\omega_o ...
...ght]} P_0(\omega_{0},{\bf k}_0;{\bf h}=0)
\EQNLABEL{dmoinv.eq}\end{displaymath}](img19.gif) |
(7) |
where
| 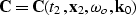 |
(8) |
Note that for consistency with our definition of the AMO operator we
consider a DMO-1 for a forward DMO that reconstructs a zero-offset
section 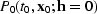 from an input section
from an input section
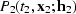 recorded at a
finite vector-offset
recorded at a
finite vector-offset 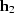 .
.
A detailed derivation of 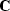 is given by Liner .
The method
is based on a general formalism (, )
for inverting integral equations
such as dmo.eq. The technique
mainly involves inserting dmo.eq into dmoinv.eq and expanding
the resulting amplitude and phase as a Taylor series and making a
change of variables according to Beylkin . The solution
provides an asymptotic inverse for dmo.eq, where the weights are given by
is given by Liner .
The method
is based on a general formalism (, )
for inverting integral equations
such as dmo.eq. The technique
mainly involves inserting dmo.eq into dmoinv.eq and expanding
the resulting amplitude and phase as a Taylor series and making a
change of variables according to Beylkin . The solution
provides an asymptotic inverse for dmo.eq, where the weights are given by
| ![\begin{displaymath}
{\bf C}=\frac {d\omega} {d\omega_o}\frac{d{\bf k}}{d{\bf k}_...
... \frac {d{\bf x}_0}{d{\bf x}_2}\right]}^{-1}
\EQNLABEL{jacob2}\end{displaymath}](img22.gif) |
(9) |
In this expression, 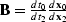 is the Jacobian of the change of variables in the forward DMO given by
is the Jacobian of the change of variables in the forward DMO given by
| ![\begin{displaymath}
{\bf B} =\frac {\partial{(t_0,{\bf x}_0)}} {\partial{(t_2,{\...
...{dt_2} & \frac {d{\bf x}_0} {d{\bf x}_2}, \end{array} \right]\ \end{displaymath}](img24.gif) |
(10) |
which reduces to 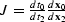 assuming the general coordinate relationships coord.relat where
assuming the general coordinate relationships coord.relat where
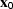 is independent of t2, leading to a zero lower left element in
the determinant matrix above.
is independent of t2, leading to a zero lower left element in
the determinant matrix above.
The quantity 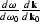 is the inverse of the Beylkin determinant, H,
is the inverse of the Beylkin determinant, H,
| ![\begin{displaymath}
H=\frac {\partial{(\omega_0,{\bf k}_0)}} {\partial{(\omega,{...
...\omega} & \frac {d{\bf k}_0} {d{\bf k}} \end{array} \right]\; .\end{displaymath}](img28.gif) |
(11) |
We actually compute the inverse of H as given by Liner :
| ![\begin{displaymath}
H^{-1}=\frac {\partial{(\omega,{\bf k})}} {\partial{(\omega_...
...}} {d{\bf k}_0} \end{array} \right]\; .
\EQNLABEL{Beylkin_inv}\end{displaymath}](img29.gif) |
(12) |
If we recognize that 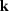 is independent of
is independent of 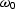 , then the lower
element of H-1 is zero and Beylkin_inv reduces to
, then the lower
element of H-1 is zero and Beylkin_inv reduces to
| 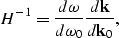 |
(13) |
where 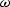 and
and 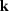 are, respectively,
are, respectively,
| ![\begin{displaymath}
\omega=\omega_o \frac {d} {dt_2} \left[ t_0(t_2) \right]
\EQNLABEL{omega}\end{displaymath}](img32.gif) |
(14) |
| ![\begin{displaymath}
{\bf k}={\bf k}_0 \frac {d} {d{\bf x}_2} \left[{\bf x}_0 ({\bf x}_2) \right]\; .
\EQNLABEL{wave.numb}\end{displaymath}](img33.gif) |
(15) |
It is very important to recognize at this stage that 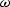 and
and 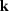 in equations omega and wave.numb depend on the coordinate
relationships coord.relat. Therefore, the Beylkin determinant, H, is
different for different DMO operators. However, as we will demonstrate later
, for kinematically equivalent DMO operators the determinant is constant.
We conclude that a general inverse DMO
is completely defined given the coordinate
relationships connecting output time and mid point
to their input values. The asymptotic inverse represents an
amplitude-preserving inverse DMO.
The methodology was first
applied to Hale's DMO by Liner and Cohen ,
and we outline
their results in the next section.
in equations omega and wave.numb depend on the coordinate
relationships coord.relat. Therefore, the Beylkin determinant, H, is
different for different DMO operators. However, as we will demonstrate later
, for kinematically equivalent DMO operators the determinant is constant.
We conclude that a general inverse DMO
is completely defined given the coordinate
relationships connecting output time and mid point
to their input values. The asymptotic inverse represents an
amplitude-preserving inverse DMO.
The methodology was first
applied to Hale's DMO by Liner and Cohen ,
and we outline
their results in the next section.
Hale DMO and its inverse
Starting from the coordinate relationships between a finite-offset data
and its equivalent zero-offset data
| 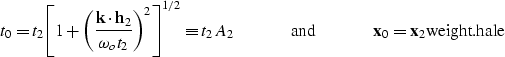 |
(16) |
After differentiating weight.hale and taking into account a factor
of 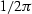 as scaling for the spatial Fourier transform we can write
jacob2 as
as scaling for the spatial Fourier transform we can write
jacob2 as
| 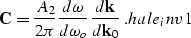 |
(17) |
The remaining task reduces to performing the necessary derivatives, and with
some algebra one can verify that H
reduces to the simple expression ()
| 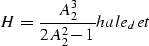 |
(18) |
and, therefore, we arrive at the inversion amplitude function
| ![\begin{displaymath}
{\bf C}=\frac {1} {2\pi} \left[1+\frac{{\bf k}^2 {\bf h}^2}{\omega_o^2t_2^2A_2^2} \right] \; .
\EQNLABEL{hale_inv}\end{displaymath}](img38.gif) |
(19) |
For a detailed derivation, the reader should refer to the original work
of Liner .
An asymptotic true inverse for Hale's DMO should then have the form:
| ![\begin{displaymath}
P_2(t_2,{\bf x}_2;{\bf h}_2)=\frac {1} {2\pi} \int d{\bf k}_...
...t]} P_0(\omega_{0},{\bf k}_0;{\bf h}=0)
\EQNLABEL{hale.inv.eq}\end{displaymath}](img39.gif) |
(20) |
Black/Zhang DMO and its inverse
Similar to the preceding discussion, we start our derivation for an
asymptotic inverse for Black/Zhang's DMO by recognizing the coordinate relationships,
| 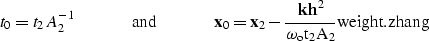 |
(21) |
The Jacobian of the change of variables in the forward DMO is given by
| 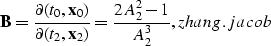 |
(22) |
which has the familiar form of Zhang's and Black's
Jacobian.
Zhang based his derivations on kinematic arguments that
considered a fixed reflection point rather than a fixed midpoint. This
derivation takes into account the reflection-point smear
(, ), which means that
the input event at location 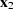 will be positioned
by DMO to the correct zero-offset location
will be positioned
by DMO to the correct zero-offset location 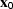 .
.
To compute the Beylkin determinant for Black/Zhang Jacobian we start by
writing the phase phase function in the DMO integral kernel as:
| 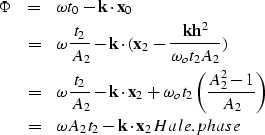 |
(23) |
| (24) |
| (25) |
| (26) |
The phase in equation Hale.phase is identical to the phase function
in Hale's DMO and, therefore, substituting for 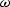 and
and 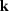 back in
omega and wave.numb and differentiating with respect to
back in
omega and wave.numb and differentiating with respect to 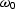 and
and 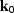 , we end up with the following expression for H-1:
, we end up with the following expression for H-1:
| 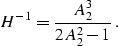 |
(27) |
Therefore, the Beylkin determinant
for Black/Zhang's DMO becomes
| 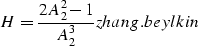 |
(28) |
which is the same as that for Hales's DMO.
Finally, by substituting back in jacob2 and accounting for the 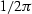 factor in the spatial Fourier transform, we obtain an expression for
the weights of an asymptotic inverse for Black/Zhang's DMO:
factor in the spatial Fourier transform, we obtain an expression for
the weights of an asymptotic inverse for Black/Zhang's DMO:
| 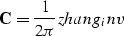 |
(29) |
These weights have been also derived independently by Paul
Fowler (personal communication).
Therefore, a true inverse for Black/Zhang's (1988) DMO has the form
| ![\begin{displaymath}
P_2(t_2,{\bf x}_2;{\bf h}_2)=\frac {1} {2\pi} \int d{\bf k}_...
...]} P_0(\omega_{0},{\bf k}_0;{\bf h}=0)
\EQNLABEL{Zhang.inv.eq}\end{displaymath}](img48.gif) |
(30) |
Bleistein Born DMO and its inverse
Starting from a different argument, Bleistein proposed
a DMO operator that he derived from a Born approximation for modeling wave
propagation. This new operator, named Born DMO (BDMO), is kinematically
equivalent to Hale's (1984) DMO and Zhang's (1988) DMO and only differs
from each of them by a simple amplitude factor. This new Jacobian
is defined as
| 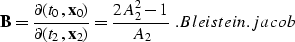 |
(31) |
Similar to the previous analysis, and recognizing that this BDMO
is kinematically equivalent to Hale's DMO, we derive the weights on the
inverse for Bleistein's operator as
| 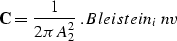 |
(32) |
An asymptotic true inverse for Born DMO is, then,
| 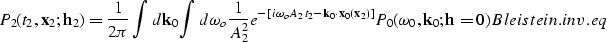 |
(33) |
Summary of true inverse for FK DMO
In this section we analyze the concept of an asymptotic true inverse
and relate it to our application of AMO.
Figures spike and comp-idmo compare results of
different inverse DMO operators.
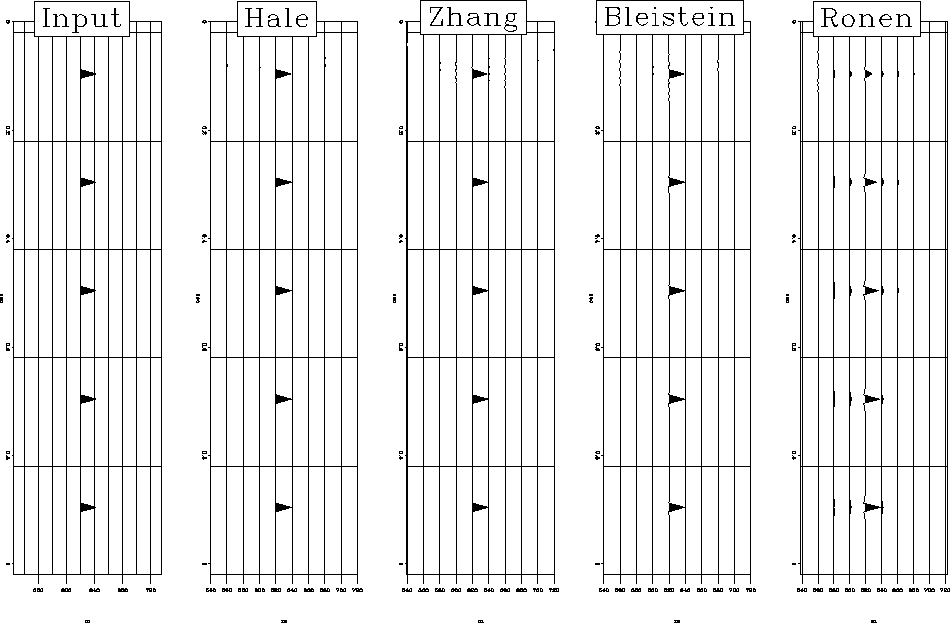
Figure spike is similar to the spike test
of Liner .
The left plot is an in-line section from a common offset cube consisting of
five unit-amplitude spikes. The offset is 800m and the CMP spacing is 20 m in
both directions. We compare the output of each true inverse
to the output of Ronen inverse.
The ideal output would be five spikes with unit amplitudes. The table below
summarizes the output of each inverse DMO for increasingly deep spikes.
Spike
Figure 1 From left to right: input data, results from Hale's inverse, Black/Zhang's inverse, Bleistein's inverse and Ronen's inverse.





| IDEAL Amp. |
Hale |
Black/Zhang |
Bleistein |
Ronen |
| 1.00 |
.76 |
.76 |
.76 |
.35 |
| 1.00 |
.95 |
.95 |
.95 |
.66 |
| 1.00 |
.97 |
.97 |
.97 |
.77 |
| 1.00 |
.97 |
.97 |
.97 |
.82 |
| 1.00 |
.98 |
.98 |
.98 |
.86 |
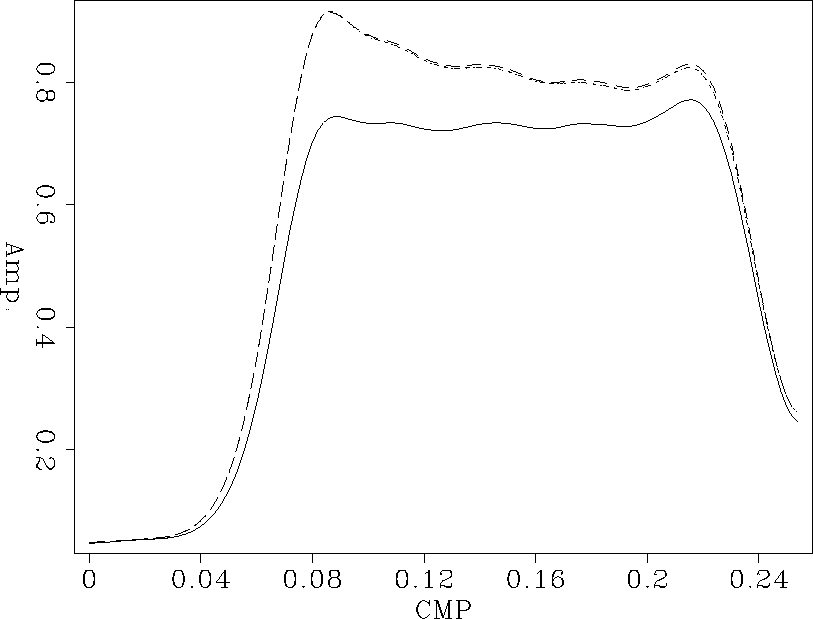
Figure comp-idmo consists of a similar test on an input earth
model consisting of a single bed dipping 35 degrees.
The original input section is a constant-offset section
recorded at half offset of 800 m with 25 m CMP spacing.
The input to each DMO-1
is the output of its corresponding forward DMO operator.
We plot the peak amplitudes picked along the dipping
event from the output of each inverse DMO.
The curves of amplitude picks from all three inverses perfectly coincide
with the amplitude picks from the original input section (DMO input).
On the same
graph we also plot the peak amplitudes extracted from the output
of Ronen's inverse. The results of this inverse clearly
fall below their expected values.
For both tests the results from the three
different DMO's analyzed were identical. This behavior follows directly
from the kinematic equivalence
of each of these DMO operators. On the spike
test we also notice that the results of the inversion are more accurate
from the shallowest to the deepest spike illustrating the asymptotic
nature of the true inverse. Note that the two tests are only conclusive on
the accuracy of the inverse DMO solution. Since we are interested
in the cascade of both forward and inverse operators acting at two different
offsets and azimuths, we need to understand what happens in the
intermediate mapping to zero offset prior to the forward modeling step.
comp-idmo
Figure 2 Peak amplitudes along the dipping event from the output of various inverse DMO algorithms. The lower amplitude curve is the result of applying Ronen's inverse. The results from Hale, Zhang, and Bleistein inverses are exactly the same and coincide with
the predicted peak amplitudes from the synthetic input.





TRUE AMPLITUDE AMO FROM TRUE AMPLITUDE DMO
Our goal is to define an amplitude-preserving AMO from a true amplitude
DMO and its true amplitude inverse. The definition of a true amplitude
inverse follows directly from an amplitude-preserving
forward operator. To select a true amplitude DMO we compare the
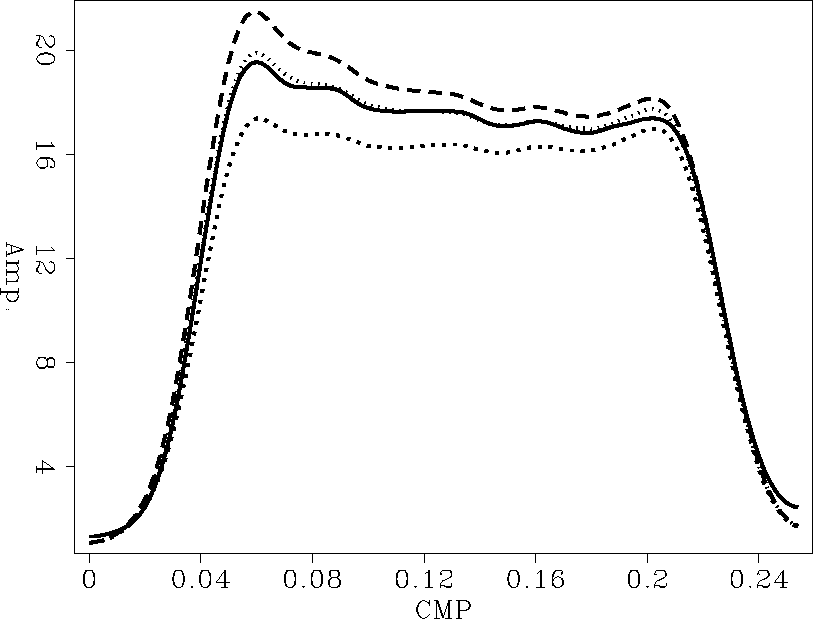
behavior of various DMO algorithms on a dipping bed. Figure comp-dmo
shows the peak amplitudes picked along
the reflection event from the output of several forward DMO operators.
The input data
is a constant offset section modeled with a 3-D Kirchhoff
style modeling algorithm. The input was corrected for
spherical-divergence spreading and for NMO
effects. On the same plot we also superimpose
the peak amplitudes from a zero-offset section generated with
the Kirchhoff modeling program.
As we notice, the theoretical curve almost coincides with the output amplitudes
of Zhang DMO. The amplitudes given by Hale's algorithm fall below the
theoretical curve whereas the peak-amplitude from Bleistein's output
overshoot the correct amplitudes. To understand this behavior we need
to examine the difference between what each DMO is trying to accomplish.
The difference between Bleistein's DMO and Black/Zhang's DMO results from
a philosophical difference about what could be
defined as ``true-amplitude DMO''.
While our goal was preserving the peak amplitude of
each reflection event, Bleistein's algorithm is based on preserving the
spectral density of the image wavelet. A second difference results from
the sequence in the processing flow surrounding DMO. A divergence
correction must be applied to the input prior to applying Black/Zhang's DMO,
whereas both input and output of Bleistein's DMO decay
with spherical divergence
factors of 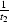 and and
and and 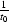 respectively
().
These two differences account for the A2 factor between the two Jacobians
leading to higher weights on Bleistein's DMO,
which results in higher peak amplitude than those on
the predicted curve.
respectively
().
These two differences account for the A2 factor between the two Jacobians
leading to higher weights on Bleistein's DMO,
which results in higher peak amplitude than those on
the predicted curve.
On the other hand, the difference between Black/Zhang's DMO and Hale's DMO
results from the fact that the former algorithm accounts for the reflection
point smear and, therefore, correctly repositions input events
at their true zero-offset
locations.
The two Jacobians differ by a factor of
| 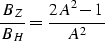 |
(34) |
Because this ratio being always larger than 1, it leads to
lower weights on Hale's operator,
which explains the lower peak amplitudes measured along the dipping event
in the output of Hale's DMO.
Consequently, to be consistent with our original definition
of ``amplitude preserved processing'', we chose to define the amplitude function
for the AMO operator from the Jacobian of Black/Zhang's DMO and the
Jacobian of its corresponding asymptotic true inverse. In the remainder of the
paper we examine the amplitude behavior of AMO according to this definition.
comp-dmo
Figure 3 Peak amplitudes along the dipping event from the output of various DMO algorithms. The continuous curve is the the predicted result, the dashed curve is Hale's result, the dotted curve is Black/Zhang's results and the large dashed curve (top curve) is Bleistein's result

AMPLITUDE PRESERVATION BY AMO
The AMO operator is defined as the cascade of an imaging operator that
acts on data with a given offset and azimuth, followed by a forward
modeling operator that reconstructs the data at a different offset and
azimuth. AMO can also be defined as the cascade of an offset continuation
operator that changes the data absolute offset followed by an azimuth
continuation operator that rotates the data azimuth. These two operations
do commute and in some applications the AMO operation may reduce to
simply one or the other.
To examine the amplitude behavior of AMO, we
conducted various numerical experiments
and tested for amplitude preservation for a
dipping reflector. In a first experiment we apply AMO as an azimuth
continuation operator to change the orientation of the input. In a second
test AMO acts a 2-D offset continuation that modifies the offset of the
data. In a final test we apply AMO as a vector-offset continuation operator
where both offset and azimuth are modified during the transformation.
For each experiment we compare the peak amplitudes picked on the
AMO reconstructed sections to the peak amplitudes extracted from identical
sections generated by synthetic modeling. To better illustrate the difference
in amplitudes, we slightly smooth the curves of amplitude picks
on both sections
Azimuth continuation
Starting from a an input constant-offset section recorded at half offset of
800 m and an angle of 5 degrees measured from the dip direction, we rotate the
azimuth of the data by 40 degrees while keeping the offset constant.
We compare the reconstructed section to a constant offset section modeled
by the 3-D modeling code at an offset of 800m and azimuth of 45 degrees.
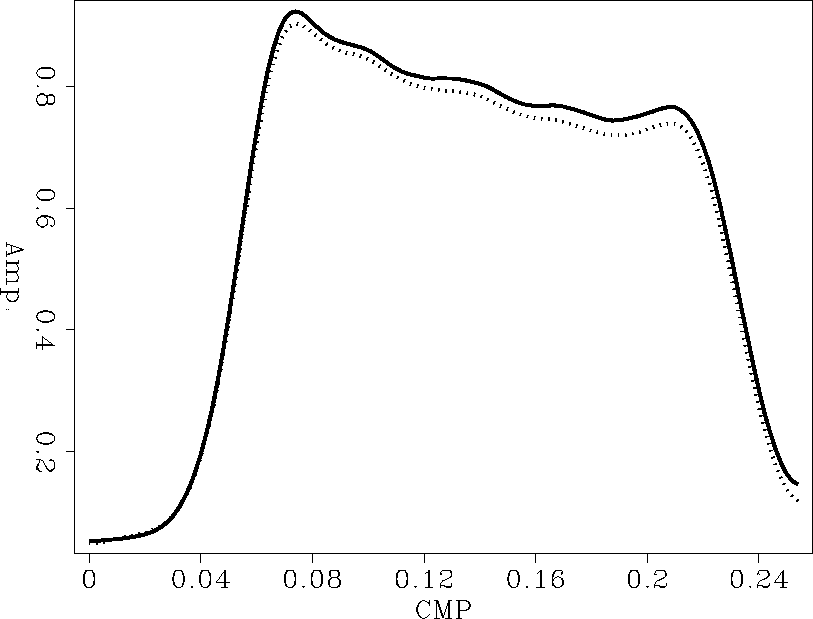
Figure azimuth shows the peak amplitudes extracted from
the output of AMO
along the dipping event.
On the same graph we also plot the peak amplitudes as picked from
the modeled section. Note that the two curves are very similar with the
reconstructed amplitudes being few percent lower than the predicted
peak amplitudes.
azimuth
Figure 4 Peak amplitudes extracted from azimuth continuated section (dashed curve) and from synthetic section (continuous plot).





Offset continuation
In the case of no azimuthal change, AMO reduces to a 2-dimensional
operator that is equivalent to an offset continuation operator. We apply
AMO to the same input constant-offset section recorded at half offset 800m
and 5-dgree azimuth to change
its offset to 400m.
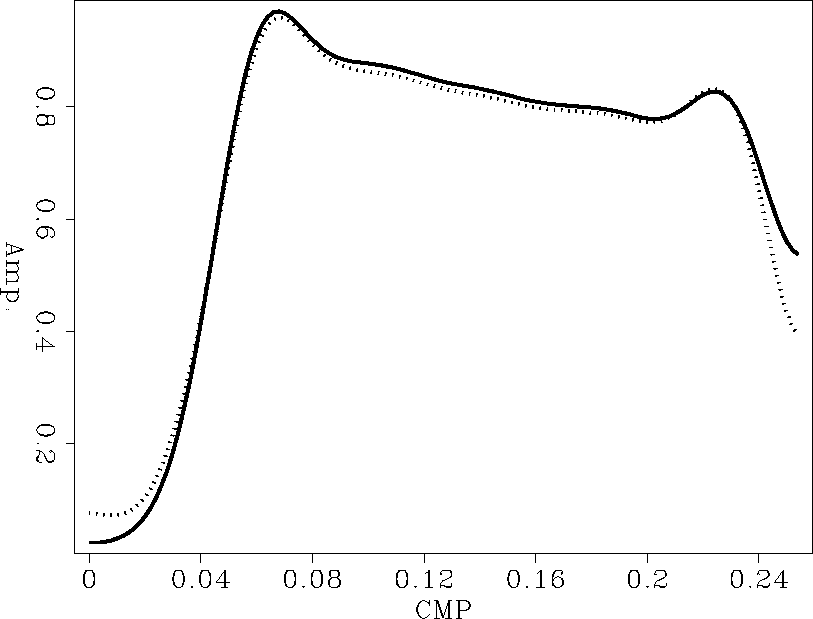
Figure offset shows the peak amplitudes picked along the dipping
event on the reconstructed section together with the theoretical curve
from the modeling program. Again we notice that both plots follow
each other very closely with an error of less than a few percent.
offset
Figure 5 Peak amplitudes from offset-continuated section from h1=800m to h2=400m and from a synthetic curve modeled at h=400m (continuous curve).





Vector-offset continuation
In a final experiment we apply the AMO operator to
transform the input constant-offset section of the first test to a
new section with different
absolute half offset of 400m and azimuth of 45 dgrees.
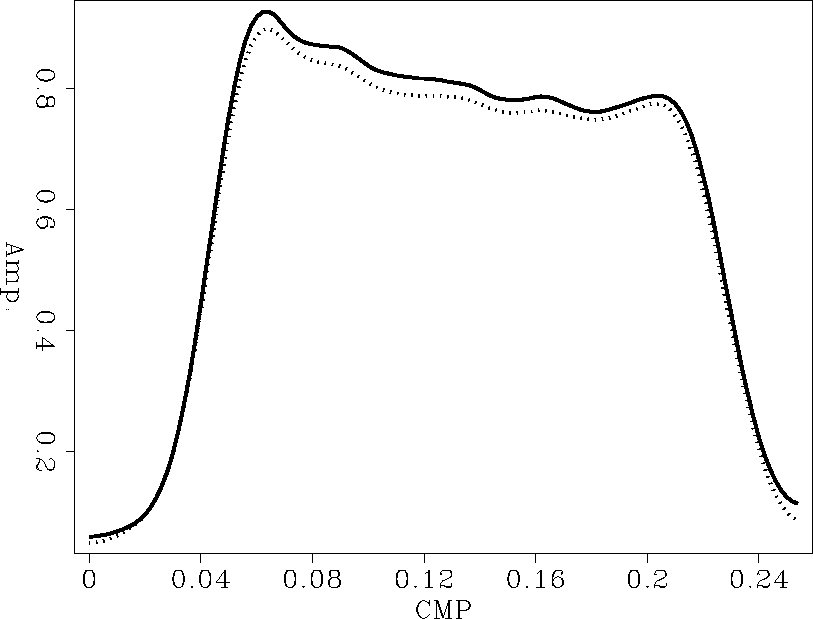
Figure amo shows the peak amplitudes picked along the dipping event
on the reconstructed section. For comparison, we also plot the peak
amplitudes from a reference section that is modeled with the same vector offset
as the output of AMO. The two curves match very closely and the differences
are more contributed to cumulative errors in the processing sequence
surrounding AMO, which includes spherical divergence
and NMO corrections prior to AMO and inverse NMO after AMO.
amo
Figure 6 Peak amplitudes extracted from a section rotated by 40 degrees and offset continuated from 800m to 400m. The solid curves shows the predicted amplitudes from the synthetic section.





CONCLUSION
We presented an amplitude-preserving function for the AMO operator.
This amplitude function is based on the FK definition of DMO
and the definition of its true inverse. Similar to Liner's formalism
of a true inverse for Hale's DMO,
we derived an asymptotically true inverse for Black/Zhang's DMO
and Bleinstein's Born DMO.
Numerical experiments showed that Black/Zhang DMO best presrves
peak amplitudes.
We define amplitude-preserved processing as the preservation of the
offset-dependent reflectivity after AMO transformation, where the
reflectivity is considered to be proportional to the peak amplitude
of each event.
We used Black/Zhang's DMO cascaded with its true inverse
to define an amplitude function for the AMO operator.
Results showed that we can preserve peak amplitudes for a dipping event
after applying AMO as an azimuth continuation operator, as an offset
continuation operator or a vector-offset transformation.
We conclude that the new AMO amplitude function represents
an amplitude-preserving azimuth moveout.
ACKNOWLEDGMENTS
We thank Norman Bleistein, Paul Fowler, Chris Liner and Mihai Popovici for
useful discussions on DMO. David lumley helped define the problem of
true amplitude processing.
A
CONNECTING FK AMO WITH INTEGRAL AMO
This appendix describes the derivation of the amplitude function for
the AMO impulse response in the time-space domain. The determinant D
in Equation amo.amp
of the main text can be written in terms of Biondi and Chemingui
notations as:
| 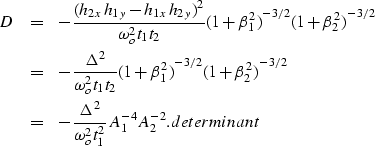 |
|
| |
| (35) |
where 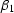 and
and 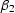 are, respectively,
are, respectively,
| 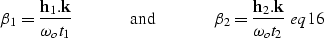 |
(36) |
and  is given by:
is given by:
| 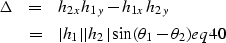 |
|
| (37) |
Using a similar change of variable as used for the solution to the stationary
path (), we write
| 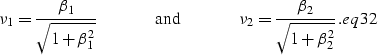 |
(38) |
where 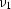 and
and 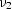 , evaluated at the stationary path
, evaluated at the stationary path 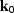 are
are
| 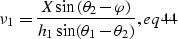 |
(39) |
and
| 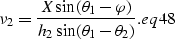 |
(40) |
Next we substitute for eq32 and eq44 in eq16 to evaluate
the determinant D at the stationary path.
In a final step we evaluate the forward and inverse Jacobaians at the stationary
path and substitute back for 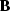 ,
, 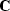 and D in
equation amo.amp of the main text. We obtain the following expressions
for the amplitude function of the AMO operator as defined in terms of
various DMO operators and their corresponding inverses.
Hale weights
and D in
equation amo.amp of the main text. We obtain the following expressions
for the amplitude function of the AMO operator as defined in terms of
various DMO operators and their corresponding inverses.
Hale weights
| 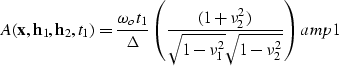 |
(41) |
Black/Zhang weights
| 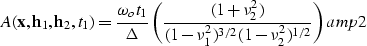 |
(42) |
Bleistein weights
|  |
(43) |
Notice that the zero-offset frequency 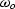 enters
as multiplicative factor in the expression for AMO amplitudes,
but the data is never available as zero-offset data during the AMO
process. The effect of this multiplicative factor can be approximated
by a time-domain filter applied either to the input or to the
output data ().
enters
as multiplicative factor in the expression for AMO amplitudes,
but the data is never available as zero-offset data during the AMO
process. The effect of this multiplicative factor can be approximated
by a time-domain filter applied either to the input or to the
output data ().
[SEP,MISC,EAEG,geophysics,paper]


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
5/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
a graphical representation of this offset transformation;
the input data with offset
shows
a graphical representation of this offset transformation;
the input data with offset
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows
a graphical representation of this offset transformation;
the input data with offset
shows
a graphical representation of this offset transformation;
the input data with offset
![]() is transformed into data with offset
is transformed into data with offset
![]() .AMO is not a single-trace to single-trace transformation,
but moves events across midpoints according to their dip.
Therefore, AMO is a partial-migration operator.
.AMO is not a single-trace to single-trace transformation,
but moves events across midpoints according to their dip.
Therefore, AMO is a partial-migration operator.
![]() and
midpoint wavenumber
and
midpoint wavenumber ![]() as
as
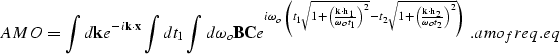
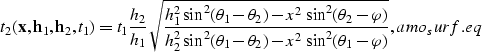
![]() and the zero-offset desired
output denoted
and the zero-offset desired
output denoted ![]() . Assume known relationships between
the coordinates of the general form
. Assume known relationships between
the coordinates of the general form
![\begin{eqnarray}
P_0(\omega_{0},{\bf k}_0;{\bf h}=0)&=&\int d{\bf x}_2 \frac {d{...
...bf x}_2)\right]} P_2(t_2,{\bf x}_2;{\bf h}_2), \
\EQNLABEL{dmo.eq}\end{eqnarray}](img18.gif)
![]() is given by Liner .
The method
is based on a general formalism (, )
for inverting integral equations
such as dmo.eq. The technique
mainly involves inserting dmo.eq into dmoinv.eq and expanding
the resulting amplitude and phase as a Taylor series and making a
change of variables according to Beylkin . The solution
provides an asymptotic inverse for dmo.eq, where the weights are given by
is given by Liner .
The method
is based on a general formalism (, )
for inverting integral equations
such as dmo.eq. The technique
mainly involves inserting dmo.eq into dmoinv.eq and expanding
the resulting amplitude and phase as a Taylor series and making a
change of variables according to Beylkin . The solution
provides an asymptotic inverse for dmo.eq, where the weights are given by
![\begin{displaymath}
{\bf B} =\frac {\partial{(t_0,{\bf x}_0)}} {\partial{(t_2,{\...
...{dt_2} & \frac {d{\bf x}_0} {d{\bf x}_2}, \end{array} \right]\ \end{displaymath}](img24.gif)
![]() is the inverse of the Beylkin determinant, H,
is the inverse of the Beylkin determinant, H,
![\begin{displaymath}
H^{-1}=\frac {\partial{(\omega,{\bf k})}} {\partial{(\omega_...
...}} {d{\bf k}_0} \end{array} \right]\; .
\EQNLABEL{Beylkin_inv}\end{displaymath}](img29.gif)
![]() and
and ![]() in equations omega and wave.numb depend on the coordinate
relationships coord.relat. Therefore, the Beylkin determinant, H, is
different for different DMO operators. However, as we will demonstrate later
, for kinematically equivalent DMO operators the determinant is constant.
We conclude that a general inverse DMO
is completely defined given the coordinate
relationships connecting output time and mid point
to their input values. The asymptotic inverse represents an
amplitude-preserving inverse DMO.
The methodology was first
applied to Hale's DMO by Liner and Cohen ,
and we outline
their results in the next section.
in equations omega and wave.numb depend on the coordinate
relationships coord.relat. Therefore, the Beylkin determinant, H, is
different for different DMO operators. However, as we will demonstrate later
, for kinematically equivalent DMO operators the determinant is constant.
We conclude that a general inverse DMO
is completely defined given the coordinate
relationships connecting output time and mid point
to their input values. The asymptotic inverse represents an
amplitude-preserving inverse DMO.
The methodology was first
applied to Hale's DMO by Liner and Cohen ,
and we outline
their results in the next section.
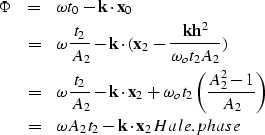
![]() factor in the spatial Fourier transform, we obtain an expression for
the weights of an asymptotic inverse for Black/Zhang's DMO:
factor in the spatial Fourier transform, we obtain an expression for
the weights of an asymptotic inverse for Black/Zhang's DMO:
![]() and and
and and ![]() respectively
().
These two differences account for the A2 factor between the two Jacobians
leading to higher weights on Bleistein's DMO,
which results in higher peak amplitude than those on
the predicted curve.
respectively
().
These two differences account for the A2 factor between the two Jacobians
leading to higher weights on Bleistein's DMO,
which results in higher peak amplitude than those on
the predicted curve.
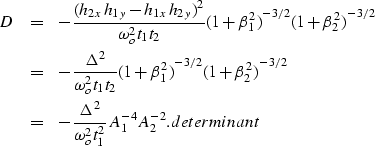
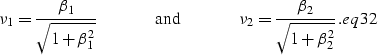
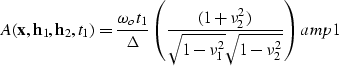
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)