![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
ABSTRACTSeismic 3-D field data is often recorded as a set of relatively sparse and often irregular 2-D lines. Under the assumption that the data consists of the superposition of local plane waves, such data can be interpolated by prediction-error techniques using a set of two 2-D filters instead of the conventional single 3-D filter. The two 2-D prediction-error filters are found by two independent linear minimization problems along sets of parallel linearly-independent lines. A third linear minimization yields the missing data. Fortunately, such an approach avoids the nonlinear minimization that is required when trying to find simultaneously the missing data and the 3-D filter on a sparse 3-D data set. |
INTRODUCTION
Interpolation of data arises whenever shortcomings in the recording geometry result in irregular, aliased, or even missing data. Claerbout discusses methods of interpolating data by data-adaptive prediction-error filters (PEF). A PEF interpolation algorithm computes the coefficients of the prediction-error filter and the missing data. If the data contains a sufficiently large, continuous patch of known data, then the filter can be found before the missing data is estimated. The data interpolation amounts to a two-stage linear optimization. If the known data does not contain such a sufficiently large continuous patch, than the filter and the missing data are estimated simultaneously by a nonlinear optimization process. The two-stage linear approach converges reliably and is therefore preferred over the nonlinear approach.
In this paper I claim that for the interpolation of 3-D data, which consists of superposed plane waves, a set of two 2-D prediction-error filters suffices. Usually, a 3-D interpolation filter is used to interpolate 3-D data. Interpolation using a single 2-D interpolation filter neglects all information along the third dimension and yields, in general, an inferior, interpolated image. I suggest, however, in this paper that a combination of two 2-D filters captures the full three dimensional information of a data set consisting of a superposition of plane waves. Claerbout proposes a similar approach for the annihilation of coherent events.
Why would anyone prefer interpolation by a pair of 2-D filters over interpolation by a single 3-D filter? Seismic data is often collected along lines. These lines are 2-D data planes in a seismic data cube, such as a shot-gather. Such a data plane is a data patch that permits the estimation of a 2-D prediction-error filter by linear optimization even when the sparseness of such lines requires a nonlinear approach for a standard 3-D filter. The method is, for example, applicable when merging overlapping 3-D surveys.
THEORY AND 1-D SYNTHETIC EXAMPLE
The test data set shown in Figure duelin
is a superposition of three functions that I call plane waves.
One plane wave looks like low-frequency horizontal layers.
The various layers vary in strength with depth.
The second wave is dipping about ![]() down to the right
and its waveform is perfectly sinusoidal.
The third wave dips down to the left
and its waveform is bandpassed random noise as in the horizontal beds.
These waves will be handled differently by different processing schemes.
To identify them clearly it may be halpful to
view the figure at a grazing angle from various directions.
down to the right
and its waveform is perfectly sinusoidal.
The third wave dips down to the left
and its waveform is bandpassed random noise as in the horizontal beds.
These waves will be handled differently by different processing schemes.
To identify them clearly it may be halpful to
view the figure at a grazing angle from various directions.
 |
Obviously we can fill in between lines by minimizing the power out of a Laplacian operator but it is better to minimize the power out of a prediction-error filter (PEF). In practice, the problem is, where do we get the PEF? Figure duelin shows an example of sparse tracks except that it is not realistic (I will use it for calibration) in the upper left corner where in a quarter circular disk the data covers the model densely. Such a dense region is ideal for determining the PEF. Indeed, the two-stage linear interpolation by a 2-D filter cannot determine a 2-D PEF from the sparse data lines because any place you put the filter (unless there are enough adjacent data lines) it will multiply missing data so every regression equation is nonlinear and abandoned.
Before we use the dense data region and before we
leap to the nonlinear regression,
there are a few tricks that get us started towards the desired result.
(When we do try a nonlinear approach
it is helpful and often essential to have a good starting guess.)
The idea is simply this:
if it is too hard to estimate a 2-D PEF,
we instead estimate a 1-D PEF,
or better yet, we estimate a 1-D PEF for
east-west tracks and a second 1-D PEF for north-south tracks.
Let ![]() be the east-west PE operator
and
be the east-west PE operator
and ![]() be the north-south operator
and let the signal or image be
be the north-south operator
and let the signal or image be ![]() .The regressions we pose are
.The regressions we pose are
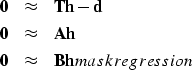 |
(1) | |
| (2) | ||
| (3) |
 |
To get the 2-D PEF, I used the two-stage linear interpolation scheme and I was dependent on the cheating corner of dense data. The purpose for cheating here is to establish motivation for the more difficult task of doing the nonlinear estimation on data lines, where cheating would be impossible. Figure duelversus compares the use of two 1-D PEFs versus a single 2-D PEF. Studying Figure duelversus, we observe that in correspondence with prediction-error theory:
3-D FIELD DATA EXAMPLE
Having demonstrated for a synthetic data case that a set of 1-D filters suffices in interpolating certain types of 2-D data, this section is going to extend the extension of this concept to the interpolation of a 3-D field data example.
Several years ago the Stanford Exploration Project collected seismic data in an experiment in the hills west of Stanford(). The geophone groups were organized out in a quadratic mesh of 13 by 13 nodes. The data cube selected for the interpolation comprises 150 time samples. The original data is displayed as 12 slices of 13 traces in Figure orig. About half of the traces of the recorded data contain no values because of instrument failure.
 |
The data geometry allows a two-stage linear interpolation approach using a 3-D prediction-error filter. The filter's extension in the (x,y)-dimensions is restricted by the size of a continuous, known data patch. The filter of the shape
a1=5 a2=3 a3=2 lag1=3 lag2=2 lag3=1
yields the interpolated data displayed in Figure miss3d.
The blank data slice in the left-hand corner of the original
data is filled in by interpolation of neighboring data slices.
Some traces are not interpolated and
I assume that the neighboring traces are inconsistent with the overall
data spectrum.
However, the prediction-error interpolation yields data that
continues the dip of the original field data and
decreases smoothly in amplitude as the interpolation distance increases.
The interpolation succeeds in the sense that the interpolated data
is hardly distinguishable from the original data.
In the following discussions I will use the interpolated data
of this 3-D interpolation approach as a reference for evaluating
the success of the subsequent interpolation schemes.
 |
In Figure missxy the data is interpolated given following two 2-D filter shapes:
a1=5 a2=3 a3=1 lag1=3 lag2=2 lag3=1
b1=5 b2=1 b3=2 lbg1=3 lbg2=1 lbg3=1
The two filters lie in the (x,z) and (y,z) data planes.
The data interpolation is of similar quality to the one in
Figure miss3d. Close examination shows that the amplitude of
the interpolated data decreases faster with interpolation
distance, than it is the case in the reference 3-D scheme.
 |
Interpolation by a set of filters in the (x,z) and (x,y) planes yield Figure missxz. The shapes of the filters are:
a1=5 a2=3 a3=1 lag1=3 lag2=2 lag3=1
c1=1 c2=3 c3=2 lcg1=1 lcg2=2 lcg3=1
Again, the prediction-error interpolation
results in a data cube comparable with the reference one in
Figure miss3d.
The rate of energy loss with interpolation distance is comparable
with the previous scheme using two vertical 2-D filters.
In the author's experience, the
horizontal filter in the (x,y) plane tends to increase the rate
of convergence when interpolating the almost horizontal event.
 |
Figure diff compares the sixth data slice of the previous interpolations. The top-right panel shows the data slice interpolated by two filters in the (x,z) and (y,z) planes. The right top panel shows the difference between the data slice to its left and the corresponding slice of the reference interpolation using a 3-D filter (Figure miss3d). The lower panel pair shows the same data slice interpolated by two filters in the (x,z) and (x,y) planes and the difference with respect to the reference data slice. There is significant energy remaining in the difference plots. The energy shows coherent linear trends which are consistent with the dip of the data.
|
diff
Figure 7 Difference plots for sixth data slice. The top row is the data interpolated by filters in the (x,z) and (y,z) planes. The bottom row is the data interpolated by filters in the (x,z) and (x,y) planes. The left column displays the difference of the interpolated data to the right with the reference data computed using a 3-D filter. |  |
Various other combinations of 2-D and 1-D prediction-error filters, such as a set of three 2-D filters in the (x,z),(y,z), and (x,y) planes, yielded comparable results to the two 2-D filter interpolation presented here.
CONCLUSIONS
In general the interpolation of certain n-dimensional data can be accomplished by a set of (n-1)-dimensional prediction-error filters. In the 2-D case, the data which is predictable (and therefore interpolated correctly) comprises horizontal events of arbitrary waveform and dipping events of sinusoidal waveform. In the 3-D case, the data which is predictable includes dipping plane waves of random waveform.
Considering a recording geometry that is continuous and dense along a sparse set of 2-D slices of a 3-D data cube, the 3-D interpolation of wavefields can be accomplished by a two-stage linear prediction-error approach. This technique allows the application of reliably converging linear inversion techniques to data sets that seem to require nonlinear interpolation. As shown in a synthetic 2-D analogue case and in a 3-D field data case, the quality of the interpolated data is roughly comparable to the quality of the standard interpolation by a single 3-D filter. In the author's experience, the computational effort for interpolation by two 2-D filters is slightly higher than the one by a single 3-D filter, when both techniques are applicable.
I conclude that if possible the prediction-error filter interpolation involving a full 3-D filter is preferable over interpolation involving a set of 2-D filters. If the sparseness of the original data prevents the application of such a 3-D two-stage linear approach, the linear two-stage approach involving a set of 2-D filters offers a valuable alternative to a nonlinear interpolation method.
[MISC,SEP]
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)