![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
ABSTRACTIn this paper I compared imaging conditions of three different prestack migrations in terms of angle-dependent reflectivity recovery. The imaging conditions compared are shot profile migration with conventional imaging condition, de Brduin's imaging condition, and planewave synthesis imaging. The conventional imaging condition can be applied to any reflector geometry and to arbitrary velocity, but it recovers only diagonal component of the reflectivity matrix. de Bruin's imaging condition recovers full reflectivity matrix but has difficulty in implementing for arbitrary reflector geometry and under variable velocity. Planewave synthesis imaging takes advantages from both conventional and de Bruin's imaging condition. |
During the past decade, the use of AVO (amplitude versus offset) analysis in petroleum exploration has become increasingly common. Even though the goal of AVO analysis is to observe the anomalous angle-dependent reflectivity behavior of a reflector, the name amplitude versus offset was chosen because most of the amplitude analysis is done in the common midpoint domain.
To analyze the properties of the reflector correctly, we need to know the angle-dependent reflectivity, which is often called AVA (amplitude versus angle). When a target reflector is close to horizontal, and velocity does not change much in the lateral direction, angle-dependent reflectivity can be obtained by measuring amplitudes along the offset, followed by ray tracing for each event to determine the corresponding incidence angle to the reflector. If a target reflector has a complex structure and strong lateral velocity variation, however, AVO may not be the same as AVA because the amplitude can be affected not only by the angle-dependent reflectivity but also by wave focusing or defocusing caused by propagation through complex velocities or structures. Resnick et al. (1987) discuss the fact that dips introduce serious problems for AVO analysis. They conclude that performing prestack migration on the data before doing AVO analysis is a necessity.
Most present day seismic migration schemes determine only the reflection coefficient of the zero offset or averaged reflectivity over a range of reflection angles for each depth point in the subsurface. This is mainly due to a simplified imaging condition.
Recently, de Bruin et al. proposed an imaging technique that produces angle-dependent reflectivity. Unfortunately, this scheme is not easy to apply when the reflector is not flat, which commonly happens in the real world.
Planewave synthesis imaging () is a promising alternative for the angle-dependent reflectivity recovery because it can be applied to any arbitrary structure and implicitly uses the same imaging condition as the one of de Bruin.
This paper describes the meaning of the image obtained by planewave synthesis migration. After reviewing the imaging conditions of the conventional prestack migration and of de Bruin et al. , I discuss the equivalence of that of the planewave synthesis imaging. Then I show some examples of angle-dependent reflectivity recovery of each imaging method using synthetic data for comparison.
THE FORWARD MODEL
Since reflectivity imaging is an inversion from seismic data collected at the surface, it is important to understand the implied forward model that relates the reflectivity to surface seismic data. After preprocessing for multiple reflections, the monochromatic 2-D forward model() for a seismic shot record can be written as follows:
| (1) |
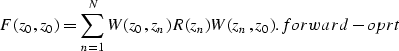 |
(2) |
In equation forward-model source vector ![]() and measurement vector
and measurement vector ![]() refer to one seismic experiment at the surface z=z0
with source location at x=xj.
In equation forward-oprt, the propagation operators
W(zn,z0) and W(z0,zn)
quantify the full propagation effects (down and up, respectively)
between depth levels z0 and zn,
and the reflectivity matrix R(zn) defines
the elastic angle-dependent reflection properties
caused by inhomogeneities at depth level zn.
All matrices and vectors refer to one temporal Fourier component.
Equations forward-model and forward-oprt
are valid for single-component
as well as multi-component measurement
of both 2-D and 3-D data ().
refer to one seismic experiment at the surface z=z0
with source location at x=xj.
In equation forward-oprt, the propagation operators
W(zn,z0) and W(z0,zn)
quantify the full propagation effects (down and up, respectively)
between depth levels z0 and zn,
and the reflectivity matrix R(zn) defines
the elastic angle-dependent reflection properties
caused by inhomogeneities at depth level zn.
All matrices and vectors refer to one temporal Fourier component.
Equations forward-model and forward-oprt
are valid for single-component
as well as multi-component measurement
of both 2-D and 3-D data ().
Propagation operators
In order to model seismic data correctly, propagation operator W should be a time extrapolation since wavefield extrapolate in time physically. However, the time extrapolation is not efficient in computation. Instead we use depth extrapolation, which is efficient in computation. If we use depth extrapolation as a propagation operator, however, we cannot model the correct amplitude of the wavefield because the energy of the wavefield in a lossless medium is preserved in time, not in depth.
This does not mean that the amplitude of wavefield obtained by depth extrapolation is totally incorrect because most of the energy recorded in reflection seismic travels near the vertical direction and the wavefield becomes a plane wave in the far distance where the energy of the wavefield is preserved both in time and depth. Therefore, if the source wavefield is a plane wave, the amplitude of the wavefield after depth extrapolation behaves similarly to that of the wavefield obtained by time extrapolation.
Reflectivity matrix
The property of the angle-dependent
reflectivity matrix R(zn) in equation forward-model
becomes clearer if we look at it in the Fourier domain
as de Bruin et al. (1990) does.
In order to obtain an expression for ![]() ,we start with the well-known angle-dependent reflection
coefficient
,we start with the well-known angle-dependent reflection
coefficient ![]() for two acoustic half-spaces separated
by an interface at zn:
for two acoustic half-spaces separated
by an interface at zn:
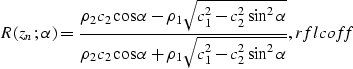 |
(3) |
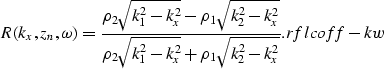 |
(4) |
As an example, Figure rc-wk-wx shows the angle-dependent
reflection coefficients in the ![]() and
and
![]() domains when c1=1500 m/s, c2=3000 m/s,
domains when c1=1500 m/s, c2=3000 m/s,
![]() , and
, and ![]() .Since the reflection is a convolution of the downgoing wavefield
with the reflection coefficient,
the reflectivity matrix in equation forward-oprt
can be visualized by taking the reflection coefficient for a given
frequency in Figure rc-wk-wx and making a matrix
whose columns are down-shifted reflection coefficients of
each other.
Figure rc-mat shows this reflectivity matrix
when
.Since the reflection is a convolution of the downgoing wavefield
with the reflection coefficient,
the reflectivity matrix in equation forward-oprt
can be visualized by taking the reflection coefficient for a given
frequency in Figure rc-wk-wx and making a matrix
whose columns are down-shifted reflection coefficients of
each other.
Figure rc-mat shows this reflectivity matrix
when ![]() .
.
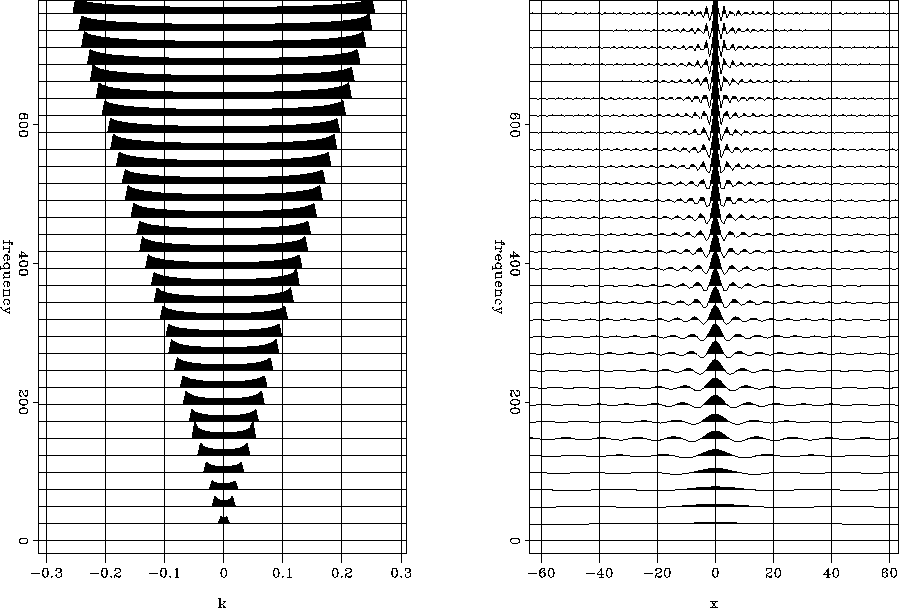 |
|
rc-mat
Figure 2 Reflectivity matrix R for | 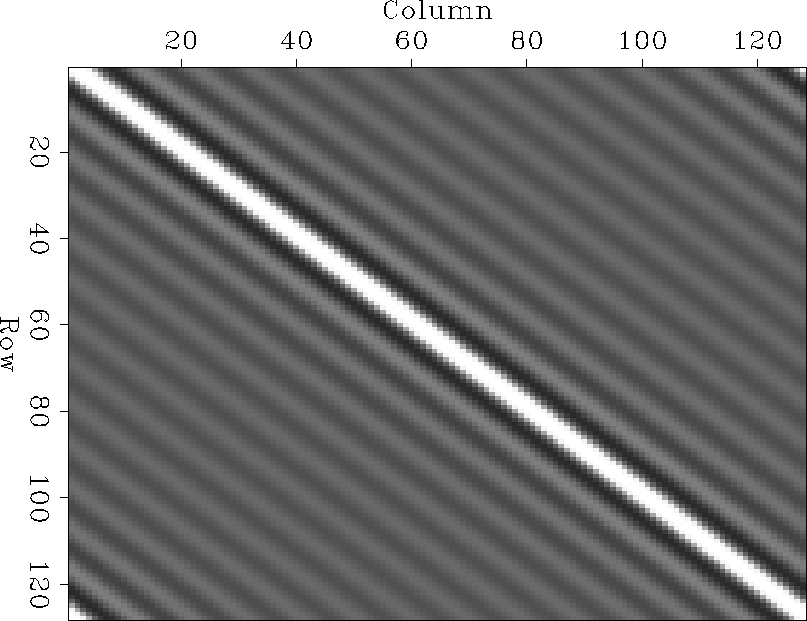 |
REFLECTIVITY IMAGING
For reflectivity imaging, we extrapolate the upcoming and downgoing wavefield recursively for each depth level as follows:
| (5) |
| (6) |
If we assume that the extrapolation operator is unitary, from the forward model forward-model we have
| (7) |
One of the most important properties of the extrapolation operator is the unitary that makes equation before-img true. Even though many algorithms based on the wave equation are accepted as unitary operators, each algorithm has a different property in terms of closeness to unitary. For this paper, I chose the split-step Fourier method () because of its pseudounitary property (Appendix A).
Conventional prestack imaging
In conventional prestack imaging as in shot profile imaging
(), the reflectivity is obtained
by deconvolving the downgoing wavefield
from the upcoming wavefield in the ![]() domain as follows:
domain as follows:
| (8) |
| (9) |
Since we performed the deconvolution in the ![]() domain
by dividing the source wave from received wave in equation cnv-imaging0,
we implicitly assumed the reflectivity matrix R is a diagonal matrix.
The diagonality of the reflectivity matrix R means locally reacting
reflection coefficient. If we assume that source wavefield
acts like a planewave locally at reflector, the imaging condition
used in the profile imaging will produce the reflection coefficient of
the angle that corresponds to the local incidence angle of the source
wavefield at each point of the subsurface.
domain
by dividing the source wave from received wave in equation cnv-imaging0,
we implicitly assumed the reflectivity matrix R is a diagonal matrix.
The diagonality of the reflectivity matrix R means locally reacting
reflection coefficient. If we assume that source wavefield
acts like a planewave locally at reflector, the imaging condition
used in the profile imaging will produce the reflection coefficient of
the angle that corresponds to the local incidence angle of the source
wavefield at each point of the subsurface.
de Bruin's imaging condition
In order to retrieve the full reflectivity matrix,
de Bruin et al. (1990) proposes another imaging condition.
Instead of deconvolving in the spatial domain,
they deconvolve in the Fourier domain ![]() after Fourier transforming both downgoing and upcoming waves,
as follows:
after Fourier transforming both downgoing and upcoming waves,
as follows:
| (10) |
| (11) |
This imaging condition retrieve the full angle-dependent reflectivity. However, since the deconvolution is performed in the Fourier domain, it implies a spatially invariant reflectivity, which is the case of horizontal reflector in constant velocity medium. Thus it has a disadvantage that is difficulty in implementing.
Imaging condition in planewave synthesis migration
In planewave synthesis imaging, the deconvolution of the downgoing wavefield from the upcoming wavefield is performed in the space domain as profile imaging does. As explained in an earlier section, the deconvolution in the space domain implies diagonality of reflectivity matrix and the diagonal property is valid only if the source wave acts like a planewave locally. This is the case of planewave synthesis migration because it synthesize a planewave source along the reflector before migration.
Therefore, in planewave synthesis migration, we retrieve the angle-dependent reflectivity by using a conventional imaging condition.
COMPARISONS WITH A SIMPLE EXAMPLE
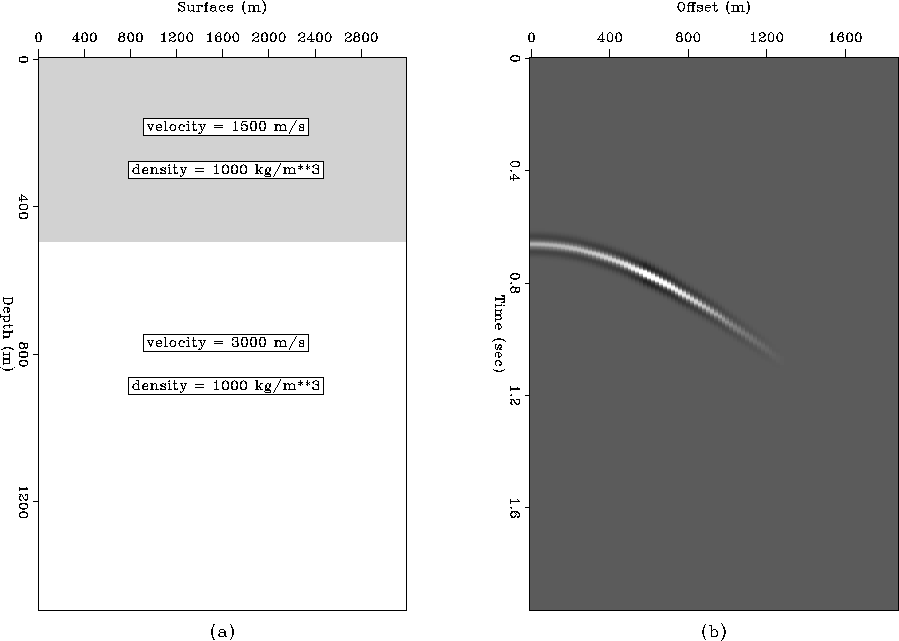
For the purposes of the comparison, let us consider the simple acoustic subsurface model shown in Figure modl-shota. Figure modl-shotb displays the simulated seismic response of one shot record and shows AVO effect clearly.
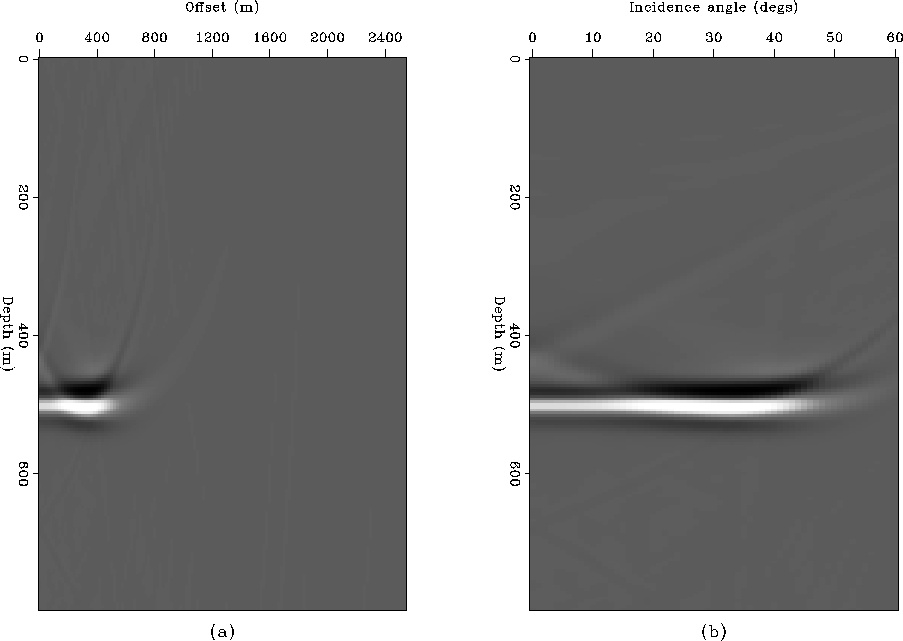
To obtain the angle-dependent reflectivity with conventional prestack imaging, I applied shot profile imaging with phase-shift extrapolation, acquired the offset-dependent reflectivity image (Figure prf-imga), and transformed it to angle-dependent reflectivity image (Figure prf-imgb) using the incidence angle to each depth location. Figure prf-db-img shows an angle-dependent reflectivity image obtained using de Bruin's imaging condition; Figure pws-img, one obtained using planewave synthesis imaging. All of them retrieve the general amplitude increasing pattern with respect to the incidence angle.
To see the amplitude more clearly, I picked amplitude of each reflectivity image at the reflector depth and plotted the amplitude as a function of the incidence angles (Figure ava). It shows the reflectivity obtained by the planewave synthesis is more close to the theoretical solution.
 |
 |
|
prf-db-img
Figure 5 Angle-dependent reflectivity image obtained by profile imaging with de Bruin's imaging condition. |  |
|
pws-img
Figure 6 Angle-dependent reflectivity image obtained by the planewave synthesis imaging. |  |
|
ava
Figure 7 Angle-dependent reflection coefficient as a function of the angle of incidence: (a) the theoretical result, (b) the result of profile imaging with conventional imaging condition, (c) the result of profile imaging with de Bruin's imaging condition, and (d) the result of planewave synthesis imaging. | 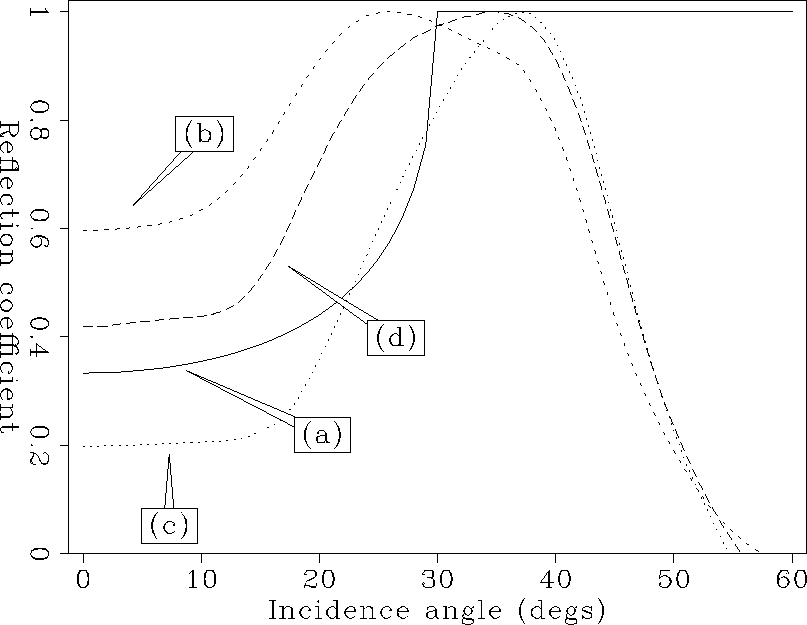 |
Although the imaging condition in planewave synthesis imaging is equivalent to that of conventional profile imaging, planewave synthesis imaging recover full reflectivity matrix as de Bruin's imaging condition. This is achieved due to the property of the source wavefield synthesized. Thus planewave synthesis imaging is a promising method to recover angle-dependent reflectivity for a nonflat reflector when lateral velocity changes. A test to a simple synthetic data showed that planewave synthesis imaging among three imaging techniques provide the closest result to the theoretical solution.
[my]
PROPERTY OF SPLIT-STEP FOURIER EXTRAPOLATION
Unitary versus Pseudounitary
A linear operator is called a unitary operator, if its adjoint equals to the inverse of it as follows:
| (12) |
| (13) |
| (14) |
Split-step Fourier extrapolation operator
Split-step Fourier extrapolation ()
consists of two-step extrapolation, which is
a phase shifting in the ![]() domain
followed by an additional phase shifting
in the
domain
followed by an additional phase shifting
in the ![]() domain.
domain.
Let us consider a simple case which consist of two depth levels extrapolation. Then the forward operator can be expressed as follows:
| (15) |
| (16) |
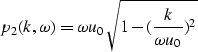 |
(17) |
| (18) |
If we apply the adjoint operator after the forward operator as follows:
| (19) |
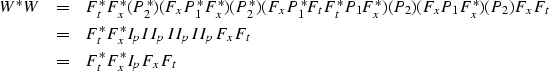 |
||
| (20) |
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)