![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Amplitude-preserved low velocity noise suppression
Hector Urdaneta
hector@sep.stanford.edu
ABSTRACT
Low velocity noise can contaminate reflections and distort AVO
amplitude information. I explore different inversion methods for
suppressing low velocity noise while simultaneously preserving
amplitudes along reflections. A velocity-stack inversion process is
used for recreating models in velocity space that can reconstruct the
reflections and the low velocity noise. Velocity-stack inversion is
the process of creating a velocity space model that can correctly
reconstruct the measured data. This is usually implemented by
minimizing the L2 norm of the data misfit and the L2 norm of the
model. Better velocity space images, with a better separation of the
reflections and the low velocity noise, can be created by minimizing a
different norm of the data misfit and a different norm of the model
length. Norms closer to the L1 norm appear to be better at
rejecting impulsive noise and creating a spiky model. Current tests
with the CORPOVEN 3-component dataset show very encouraging results.
|
Low velocity noise such as ground roll and air-waves contaminate
reflection land data and distort AVO amplitude information. Many low
velocity noise suppression techniques focus on the kinematics, e.g.,
predictive deconvolution or f-k filtering, without necessarily
preserving amplitude information. Recently, the general increase in
use of amplitudes in applications such as AVO analysis has increased
the need for amplitude-preserved low velocity noise and multiple
suppression ().
intro
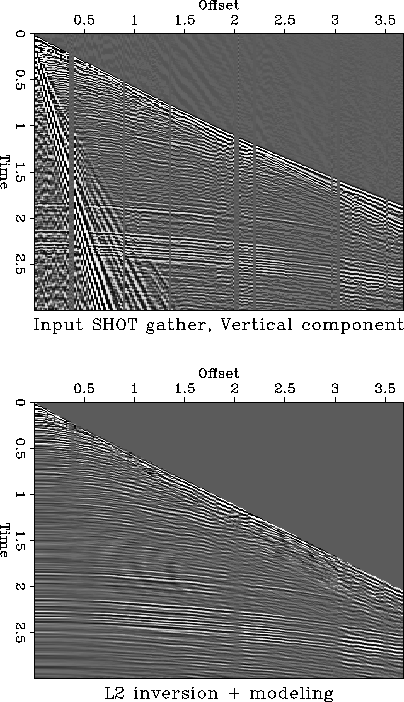
Figure 1 Top: Field shot gather from the
CORPOVEN 3-component dataset (Ata et al., 1994). Bottom:
reconstructed shot gather after suppression of low velocity noise,
product of an L2 velocity-stack inversion of the field shot
gather, muting of the low velocity noise in velocity-stack space,
and remodeling of the signal. Finally a linear outer mute of
1.8 km/s has been applied to the gather.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





The top frame of Figure intro defines the problem. It shows a
shot gather in which the events of interest are contaminated with low
velocity noise at low offsets, distorting the AVO amplitude
information. The bottom frame of Figure intro illustrates the
solution I am looking for, that is, the ability to separate the
interference between the noise and the the events of interest (from
here on called ``the signal'') without affecting the AVO information.
With this goal in mind, I began by looking for an operator whose
range has axes of time and offset, whose domain's representation of
the signal and noise can be best separated, and which has an efficient
and stable inverse.
Two schemes for suppressing the low velocity noise are available. The
first is modeling of the signal and the second modeling of the
noise. The motivation for modeling the signal is to get the best
representation of the signal and to mute the noise in the operator's
domain in order to reconstruct only the signal. The reason for
modeling the noise is that by doing so I mute the signal in the
operator's domain to reconstruct only the noise, and then subtract it
from the data in order to obtain the signal. In modeling the signal
there is a risk that any part of the signal that is not correctly
reconstructed may artificially distort the amplitudes, which will
disturb the AVO analysis. Nevertheless, modeling the signal proves to
be easier than modeling correctly the noise because of the
spatial aliasing of the noise.
Two processing operators are candidates for carrying out these two
schemes: velocity-stack, for modeling the signal, and slant-stack, for
modeling the noise. The advantage of using these two processing operators,
in contrast to using physical operators, is that we are completely
free to modify them to optimize our processing goal, since they have
no constitutive relations that they need to satisfy. In this case it
may be useful to modify the operators to make them more easily
invertible (), to accelerate convergence
(), or to modify the inversion norm to obtain
spiky models ().
The velocity-stack operator has the disadvantage of not having an
analytic inverse or a simple inverse. However, it is possible to
implement the inverse transform using an iterative solver. Usually,
the inverse transform is implemented as the minimization of a
least-squares problem. The least-squares solution has some attributes
that may be undesirable. In this paper I show the use of other types
of norms in suppressing low velocity noise, following Nichols'
steps for suppressing multiples. I explore
the use of slant-stack inversion for modeling the noise on a synthetic
example, and the use of velocity-stack inversion for modeling the
signal on both a synthetic and a real example.
MODELING THE SIGNAL
As discussed above, the modeling of the signal is done with a
velocity-stack operator because of the hyperbolic nature of the
reflector in the gathers offset vs. time space, which produces a
localized model representation of the signal in the velocity-stack
space. Stacking operators are processing tools that may map data to an
unphysical domain that happens to be convenient for processing
reasons. The normal gather domain has axes of time and offset. The
stack domain has axes of zero-offset time and velocity or
slowness. Although the stacking space is unphysical, and these
operators can not be derived from constitutive relations of physics,
they are convenient since many data processing applications are much
simpler in the stacking domain. For example, the low velocity noise
may be isolated and muted in velocity-stack space, allowing
reflections to be enhanced in the processed version of the input
seismic data.
In doing velocity-stack inversion the aim is to create a model in the
velocity-stack space in which the signal energy and the noise energy
are well separated. In addition, the reconstructed data must be a good
match to the signal-only part of the original data. In this section I
explore modeling the signal using a velocity-stack operator. I first
try using an L2 inversion and then other inversion norms that
produce more pleasing results. As an example, I use a synthetic
gather that depicts some of the events seen in any of the vertical
component shot gathers of the CORPOVEN 3-component dataset.
Least squares inversion
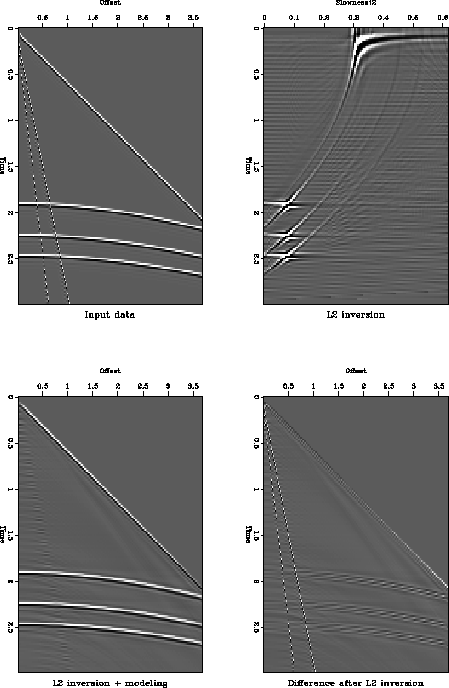
Figure L2synth displays four stages in the processing of a
synthetic gather. The first frame is the original data, 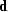 ,consisting of three hyperbolic events, direct arrival, and two aliased
events that depict the arrival of very low velocity surface waves. The
second frame is its L2 velocity-stack inverse, the third frame is
the data remodeled from the inverse, and the final frame is the
difference between the input synthetic and the remodeled data. The
hyperbolic events of the original data are contaminated by the low
velocity noise at low offsets.
,consisting of three hyperbolic events, direct arrival, and two aliased
events that depict the arrival of very low velocity surface waves. The
second frame is its L2 velocity-stack inverse, the third frame is
the data remodeled from the inverse, and the final frame is the
difference between the input synthetic and the remodeled data. The
hyperbolic events of the original data are contaminated by the low
velocity noise at low offsets.
L2synth
Figure 2 L2 inverse processing. Top
left: input data. Top right: velocity-stack inverse using an L2
norm of the data misfit. Bottom left: reconstructed input
data. Bottom right: residual data not modeled.




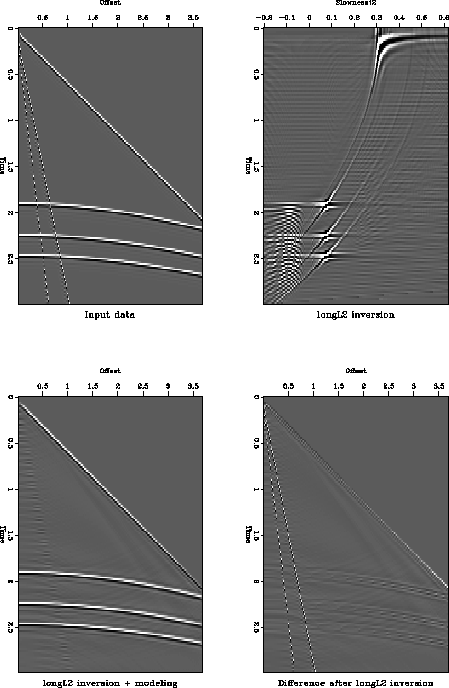
 longL2synth
longL2synth
Figure 3 L2 inverse processing
using a wider-slowness squared range to include negative values. Top
left: input data. Top right: velocity-stack inverse using an L2
norm of the data misfit. Bottom left: reconstructed input
data. Bottom right: residual data not modeled.





In the second frame of Figure L2synth I have solved the inverse
problem to
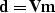
where  is the
velocity-stack space model and
is the
velocity-stack space model and 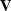 is the forward operator that
maps from velocity-stack space to offset space. For the inverse
problem I seek a solution to the problem of finding the model in
velocity-stack space,
is the forward operator that
maps from velocity-stack space to offset space. For the inverse
problem I seek a solution to the problem of finding the model in
velocity-stack space,  , given the data,
, given the data, 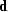 . This is
usually posed as a least-squares minimization problem that minimizes
the energy of the misfit between the modeled and measured data:
. This is
usually posed as a least-squares minimization problem that minimizes
the energy of the misfit between the modeled and measured data:
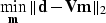
The use of a conjugate gradient method in performing the inversion
will not only minimize the data misfit but will also minimize the
energy of the solution:
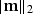
Figure L2synth shows the result of the L2 minimization of the
data misfit's norm. By limiting the domain of the velocity-stack
operator to low-slowness squared values and excluding the
corresponding high slowness representation in the velocity-stack space of
the low velocity noise, I am able to suppress the noise. Because I
do not define sufficiently well where the energy of the signal lies in
the the velocity-stack space, I am not able to model the signal at
large offsets correctly, since we see some smearing of the signal in the
residual part of the data not modeled. Moreover, we see that the noise
is not completely removed.
In Figure longL2synth I have extended the domain of the
velocity-stack operator to include negative-squared slownesses, which
model positive curvature hyperbolas. This models the signal at large
offsets more successfully, but does not yield a perfect result. Adding
negative-squared slownesses to the velocity-stack domain is only
possible because velocity-stack is a processing operator; it does not
need to satisfy any physical laws.
Weighting the residual
We can also choose to minimize the Lp norm of the residual by minimizing
the weighted residual
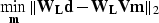
where 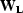 is a diagonal operator whose ith component is
a function of the residual vector
is a diagonal operator whose ith component is
a function of the residual vector
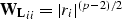
This is equivalent to solving the weighted problem
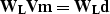
This scheme minimizes the Lp norm of the data misfit and the L2
norm of the model space
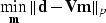
and
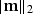
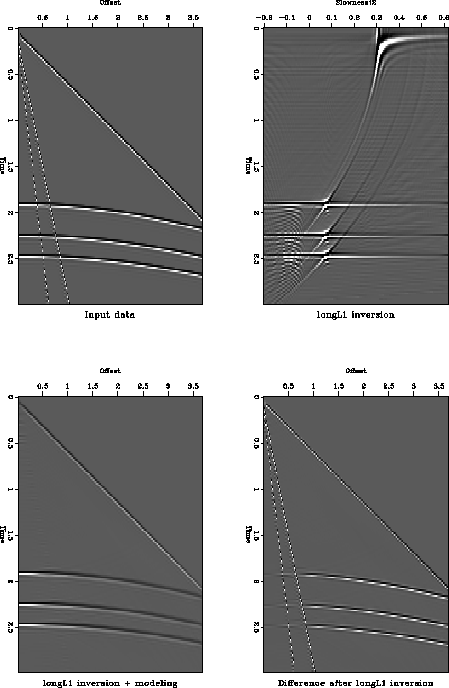
Figure longL1synth shows the result of using an L1.1 norm
to do minimize the data misfit. We see that the model is less
noisy, yet the model representation of the three hyperbolic
events are spread outside the domain of the velocity-stack
operator. This results in a sharper image of the modeled signal, but
there is a higher loss of the signal as we go to further offsets.
longL1synth
Figure 4 L1.1 inverse processing. Top
left: input data. Top right: velocity-stack inverse using an
L1.1 norm of the data misfit. Bottom left: reconstructed input
data. Bottom right: residual data not modeled.





Weighting the model
By combining model space weights and data space weights we can
minimize the Lp norm of both the data misfit and the model space.
In order to do this I solve the problem
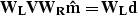
followed by
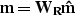
where 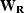 is the diagonal operator whose ith component is
is the diagonal operator whose ith component is
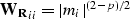
This scheme minimizes the Lp norm in both the data misfit and the
model space:
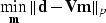
and
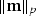
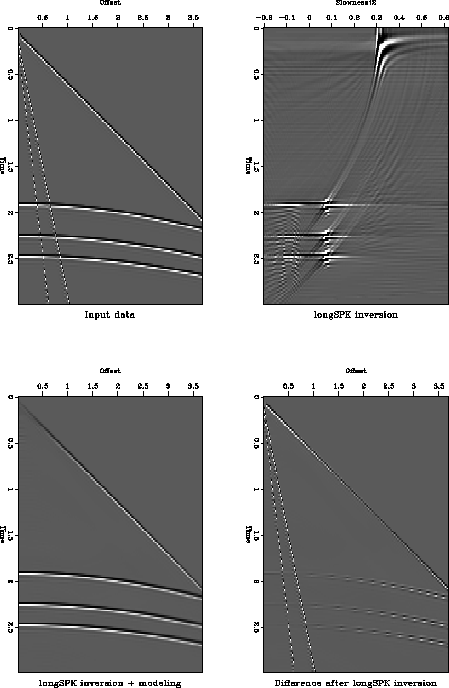
Figure longSPKsynth shows the result of using an L1.5 norm
in both domains. We see how I get a spiky velocity-stack model of the
signal, which reconstructs a nicer signal, but there is some loss of
signal energy at far offsets. It is encouraging that the noise has
been totally removed from the reconstructed data.
longSPKsynth
Figure 5 Spiking inverse processing.
Top left: input data. Top right: velocity-stack inverse using an
L1.5 norm of the data misfit and L1.5 norm of model length.
Bottom left: reconstructed input data. Bottom right: residual data
not modeled.





MODELING THE NOISE
Modeling the low velocity noise is done using a slant-stack operator,
which produces a localized noise representation in the slant-stack
velocity space, because of its linear nature in the gather offset
vs. time space. The goal of modeling the noise is that if I model it
well, I can subtract it from the input data and obtain the signal
without worrying about distorting the signal's amplitude. The aim of
the slant-stack inversion is to separate as best as possible the model
representations of the signal and noise.
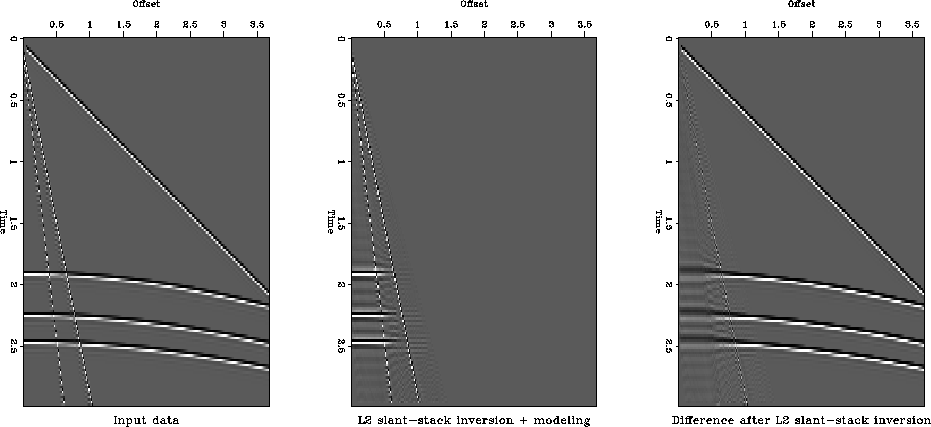
Figure ss1diff.L2 shows the result of using an L2 norm for
inverting the problem
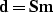
where  is
the slant-stack space model and
is
the slant-stack space model and 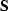 is the forward operator that
maps from slant-stack space to offset space. Just as in the inverse
problem for modeling the signal, I seek a solution to the problem of
finding the model in slant-stack space,
is the forward operator that
maps from slant-stack space to offset space. Just as in the inverse
problem for modeling the signal, I seek a solution to the problem of
finding the model in slant-stack space,  , given the data,
, given the data,
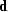 .
.
The middle frame of Figure ss1diff.L2 shows the reconstructed
data from the slant-stack space model (not shown) and the right frame
shows the data not reconstructed. We see that I am only able to
reconstruct the unaliased energy of the noise while the aliased energy
still contaminates the signal, so I have not succeeded in removing
the low velocity noise. Even worse we notice how part of the
signal gets modeled at low offsets; this is due to applying the
stacking operator along the offset axis as is conventionally done.
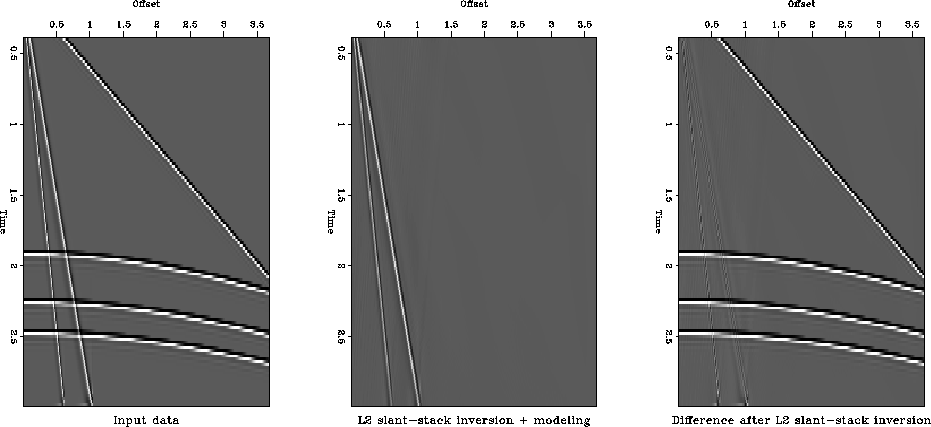
To prove this last statement, I have done the stacking along the time
axis, which eliminated completely the reconstructed signal at low
offsets as illustrated in Figure ss2diff.L2. Moreover I have
dealiased the low velocity noise to show that to a very good extent, I
have been able to suppress the low velocity noise from the data
without distortion along the amplitude of the signal.
ss1diff.L2
Figure 6 L2 slant-stack L2
inverse processing. Stacking done along offset axis. Left: input data,
low velocity noise is aliased. Middle: reconstructed input
data. Right: residual data not modeled.




 ss2diff.L2
ss2diff.L2
Figure 7 L2 slant-stack L2
inverse processing. Stacking done along time axis. Left: input data,
low velocity noise is unaliased. Middle: reconstructed input data
(suppressed low velocity noise). Right: residual data not modeled
(amplitude-preserve signal).





REAL DATA EXAMPLE
Figures ss1diff.L2 and ss2diff.L2 have illustrated the
point made in the introduction that even though it is more desirable
to model the noise, this is only true to the extent that we can
dealias the noise. Since I do not have the right tool to dealias
the low velocity noise, in the following real data examples, I have
chosen to model the signal as a means of suppressing the low velocity
noise.
The following figures show the effect of using the various inversion
methods on a shot gather from the 3-component dataset provided by
CORPOVEN.
()
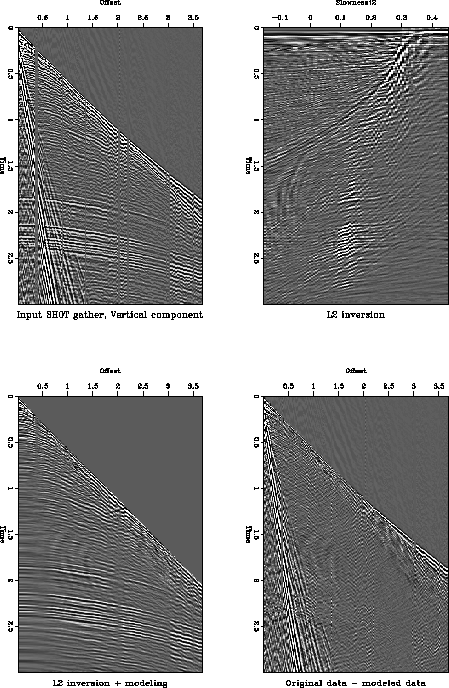
Figure real2p.L2 displays the four
stages in the processing of a vertical component shot gather. The
first frame is the raw shot gather, the second frame is its L2
velocity-stack inverse, the third frame is the signal reconstructed
from the inverse, and the fourth frame is the difference between the
raw shot gather and the reconstructed data. I chose to process the
raw data in shot gather space instead of CMP space, since in CMP space
the spatial aliasing of the low velocity noise will be even greater
as a result of the bigger spacing between traces in CMP space.
The CORPOVEN shot gathers are sampled at 2 msec intervals with a 6
second record length. The number of receivers per shot is 216, with a
geophone group interval of 17 meters. The most relevant events occur
at about 1.9, 2.1, and 2.2 seconds. The data is very rich in low
velocity noise, but because it has a distinct RMS-stacking
velocity from the signal, the muting of the noise in the
velocity-stack space does an excelent job of removing it from the
reconstructed signal, as we see from the third and fourth frames in
Figure real2p.L2. There is some energy loss of the signal at far
offsets, as we can see (if we look at the plot at an angle) in the
fourth frame at around 2.5 kms.
real2p.L2
Figure 8 L2 inverse processing. Top
left: input shot gather, vertical component. Top right:
velocity-stack inverse using an L2 norm of the data misfit and
negative squared slownesses. Bottom left: reconstructed input
data. Bottom right: residual data not modeled.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





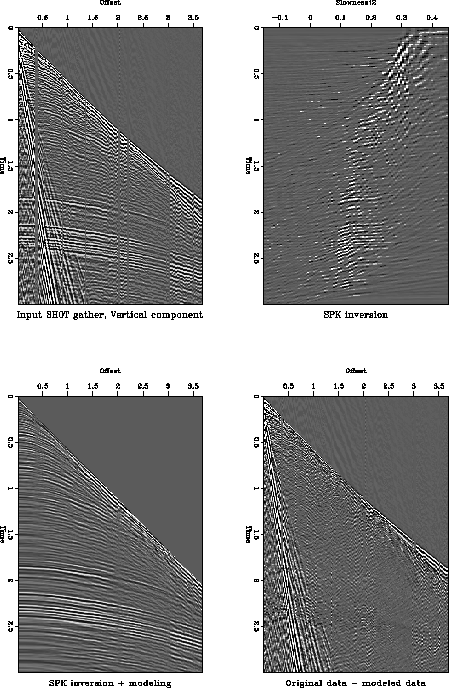
Figure real2p.SPK displays the effect of spiking inversion in
the model space. The inversion minimized the L1.1 norm of the
data misfit and the L1.1 norm of the model. The events in
velocity-stack space are much more compact. This is a very desirable
result, since I now obtain a better reconstruction of the signal,
while suppressing completely the low velocity noise from the
reconstructed data.
real2p.SPK
Figure 9 Spiking inverse processing.
Top left: input shot gather, vertical component. Top right:
velocity-stack inverse using an L1.1 norm of the data misfit and
L1.1 norm of model length. Bottom left: reconstructed input
data. Bottom right: residual data not modeled.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





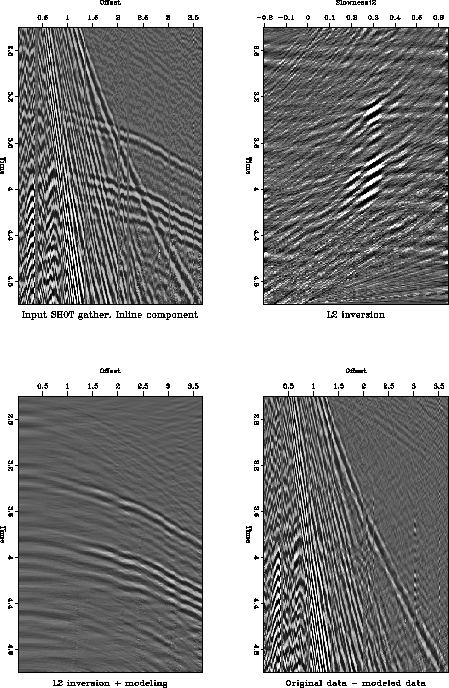
Figure real2v.L2 shows the same four processing stages of the
shot gather's inline component. The first frame shows a windowed
section of the gather, which is heavily contaminated with low velocity
noise. It is interesting to note the dispersion of the ground
roll. The higher frequencies (which are aliased), arrived first, while
the lower frequencies (which are unaliased), arrived later. The second
frame is the L2 velocity-stack inverse and the third and fourth
frames are the reconstructed data and the difference between the raw
data and the reconstructed data, respectively. Even though the
amplitudes reconstructed at near offsets are somewhat questionable,
since the noise level at near offsets is so high that it completely
masks away the signal, the inversion does a good job reconstructing
the signal at mid and far-offsets. Looking at the reconstructed data
at an angle, we can see that the reconstructed reflections at low
offsets are more evident.
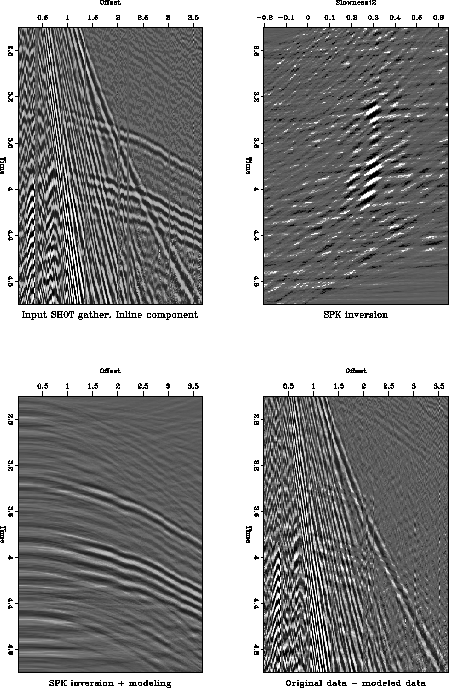
Figure real2v.SPK shows the use of a spiking inversion of the
gather's inline component to suppress the low velocity noise, which
produces a more spiky velocity-stack model.
real2v.L2
Figure 10 L2 inverse processing. Top
left: input windowed shot-gather, inline component. Top right:
velocity-stack inverse using an L2 norm of the data misfit and and
negative squared slownesses. Bottom left: reconstructed input
data. Bottom right: residual data not modeled.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)




 real2v.SPK
real2v.SPK
Figure 11 Spiking inverse processing.
Top left: input windowed shot-gather, inline component. Top right:
velocity-stack inverse using an L1.1 norm of the data misfit and
L1.1 norm of model length. Bottom left: reconstructed input
data. Bottom right: residual data not modeled.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





I have discussed two methodologies for suppressing low velocity noise
while preserving signal amplitudes. The techniques involved the use of
different minimization norms for the data misfit and the model length.
Velocity-stack inversion is used to reconstruct the signal, and
slant-stack inversion is used to reconstruct the noise. The complete
liberty to modify these processing operators and the use of norms
closer to L1 produce more desirable velocity space images, with a
better separation of the signal energy and the low velocity noise
energy. For the real data examples, forward modeling of the
velocity-stack space images produce an amplitude-preserved low
velocity noise suppression. Current tests with the CORPOVEN
3-component dataset appear very encouraging.
ACKNOWLEDGMENTS
Thanks to Eulogio DelPino of CORPOVEN and Reinaldo Michelena and
Manuel Gonzáles of Intevep for providing me with the CORPOVEN
multicomponent dataset. I am grateful to David Lumley and Biondo
Biondi for the many productive discussions about this topic. Dave
Nichols' C++ solvers and operators developed for suppressing
multiples were easily modified and used for suppressing the low
velocity noise. Vive le C++!
[SEP,SEGCON,GEOTLE,SEGBKS,MISC,hector]


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
5/9/2001
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)