




Next: The Crank-Nicolson method
Up: Mo: Numerical analysis
Previous: UNDERMIGRATION CAUSED BY PARABOLIC
Equation (5) can be transformed into the space-frequency domain,
resulting in the 15-degree 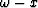 time migration equation
time migration equation
| 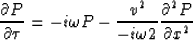 |
(6) |
This partial differential equation can be solved by splitting it
(Claerbout, 1985) into the diffraction term
| 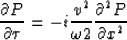 |
(7) |
and the lens term
| 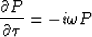 |
(8) |
The lens equation can be solved accurately by analytic exponentiation.
Here I consider the diffraction equation, which is a
partial differential equation (PDE). A PDE can be readily converted to a
system of ordinary differential equations (ODEs) by using finite-difference
approximations for derivatives in all but one of the dimensions.
To do so, I discretize coordinate x with N+1 uniformly spaced grid points,
as follows:
| 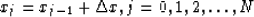 |
(9) |
Using the second-order central-difference scheme for the second derivative in
x results in
| 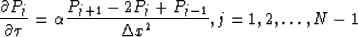 |
(10) |
where 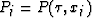 and
and 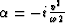 .
With a further assumption of the boundary condition
.
With a further assumption of the boundary condition 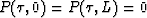 ,
I obtain a system of
ODEs that can be written in matrix form as
,
I obtain a system of
ODEs that can be written in matrix form as
| 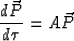 |
(11) |
where Pj's are the elements of the vector 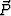 , and A is the
(N-1)*(N-1) tri-diagonal matrix
, and A is the
(N-1)*(N-1) tri-diagonal matrix
|  |
(12) |
This system of ODEs can be solved using any of the numerical methods, such as
the Runge-Kutta formulas or multi-step methods.
However, when dealing with systems,
we need to be concerned about stiffness. To investigate numerical stiffness,
we must study the eigenvalue structure of the matrix A.
The eigenvalues of A
obtained from a known formula for the eigenvalues of a tri-diagonal
matrix with constant entries are
| 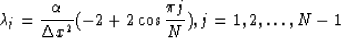 |
(13) |
It is important to keep in mind that all the eigenvalues of A are non-zero
and purely imaginary, since  is purely imaginary.
The eigenvalue with the smallest magnitude is
is purely imaginary.
The eigenvalue with the smallest magnitude is
| 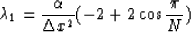 |
(14) |
For large N, the series expansion for 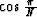 ,
,
| 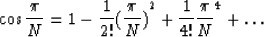 |
(15) |
converges rapidly. Retaining the first two terms in the expansion results in
| 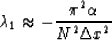 |
(16) |
Also, for large N
| 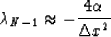 |
(17) |
Therefore, the ratio of the eigenvalue with the largest modulus to the
eigenvalue with the smallest modulus is
| 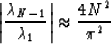 |
(18) |
Thus for seismic migration, typically 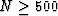 traces,
this is an extremely stiff system of ODEs.
There is severe contradiction in choosing the
pseudodepth (time
traces,
this is an extremely stiff system of ODEs.
There is severe contradiction in choosing the
pseudodepth (time  ) step size of downward extrapolation,
so that explicit methods, for example, explicit Euler and Runge-Kutta methods
are unworkable.
) step size of downward extrapolation,
so that explicit methods, for example, explicit Euler and Runge-Kutta methods
are unworkable.
Standard decoupling using the matrix of eigenvectors S yields
| 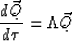 |
(19) |
where 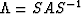 is a diagonal matrix with the eigenvalues of A on
the diagonal, S is the matrix whose columns are the eigenvectors of A,
and
is a diagonal matrix with the eigenvalues of A on
the diagonal, S is the matrix whose columns are the eigenvectors of A,
and 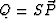 . Since the equations are uncoupled,
the following solution can be readily obtained:
. Since the equations are uncoupled,
the following solution can be readily obtained:
| 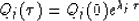 |
(20) |
Thus, purely imaginary eigenvalues result in the oscillation of the solution
that is expected for the wave equation.





Next: The Crank-Nicolson method
Up: Mo: Numerical analysis
Previous: UNDERMIGRATION CAUSED BY PARABOLIC
Stanford Exploration Project
11/17/1997

![]() traces,
this is an extremely stiff system of ODEs.
There is severe contradiction in choosing the
pseudodepth (time
traces,
this is an extremely stiff system of ODEs.
There is severe contradiction in choosing the
pseudodepth (time ![]() ) step size of downward extrapolation,
so that explicit methods, for example, explicit Euler and Runge-Kutta methods
are unworkable.
) step size of downward extrapolation,
so that explicit methods, for example, explicit Euler and Runge-Kutta methods
are unworkable.