Next: Future work
Up: WAVE-EQUATION DATUMING ALGORITHM
Previous: Wave-equation Datuming for laterally
To illustrate the datuming algorithm I use several velocity
models. I use the topographic surface displayed in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The reflectivity model consists of a syncline in the middle of a horizontal layer.
In order to analyze how the datuming algorithm affects
the initial data I apply the conjugate pair of datuming operators and
compare the resulting data with the initial data.
.
The reflectivity model consists of a syncline in the middle of a horizontal layer.
In order to analyze how the datuming algorithm affects
the initial data I apply the conjugate pair of datuming operators and
compare the resulting data with the initial data.
datum
Figure 3 The surface topography (datum) used for the datuming examples.
|
|  |

The initial data is the result of zero-offset modeling using
the syncline reflectivity model with different velocity models.
The zero-offset data is obtained on a flat datum. Figure
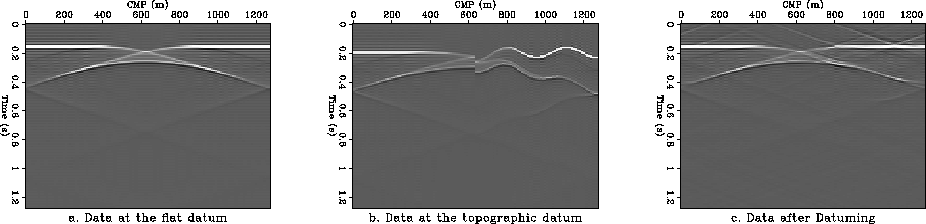
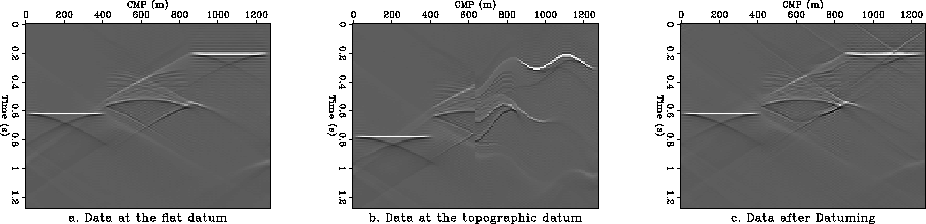
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows an example for a constant velocity medium.
The zero-offset data is then extrapolated to the uneven topographic datum
shown in Figure
a shows an example for a constant velocity medium.
The zero-offset data is then extrapolated to the uneven topographic datum
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to obtain the data in Figure
to obtain the data in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
Using the conjugate transpose algorithm, data is extrapolated back
to the flat datum to obtain the third panel in Figure
b.
Using the conjugate transpose algorithm, data is extrapolated back
to the flat datum to obtain the third panel in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
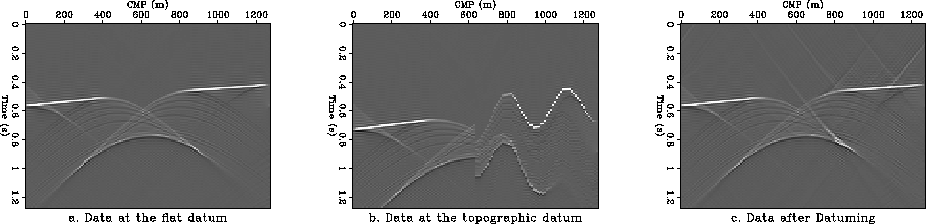
By comparing the first and the third panel in Figure
c.
By comparing the first and the third panel in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we
can estimate the effect of the datuming algorithm on the initial data.
we
can estimate the effect of the datuming algorithm on the initial data.
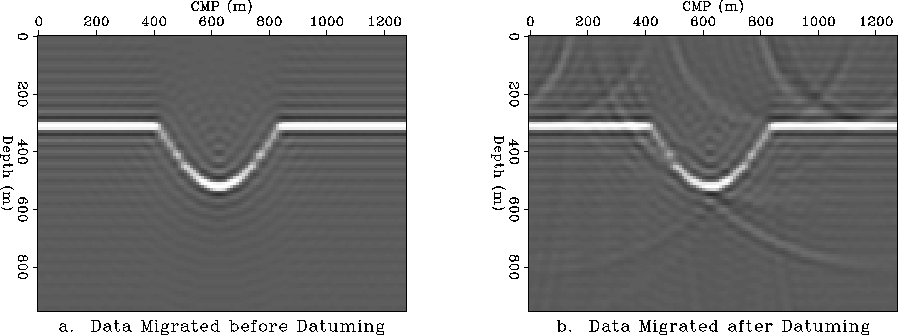
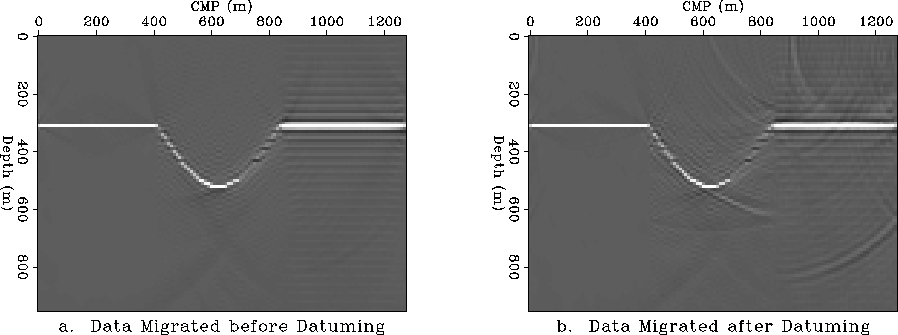
The initial zero-offset data is migrated prior to the datuming step
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and then again after the pair of
conjugate datuming operators is applied. The migrated image
after conjugate datuming is shown in Figure
a and then again after the pair of
conjugate datuming operators is applied. The migrated image
after conjugate datuming is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
b.
I use several velocity models for assessing the effects of
the datuming algorithm on zero-offset data. The first velocity
model, used to obtain Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
is just constant. The next model, used to obtain Figures
,
is just constant. The next model, used to obtain Figures
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , is a linearly increasing
velocity in depth
, is a linearly increasing
velocity in depth ![$v(z)=1000.+0.6 z \: [m/s]$](img34.gif) . The third velocity model
is linearly increasing both in depth and laterally
. The third velocity model
is linearly increasing both in depth and laterally
![$v(x,z)=1000.+0.6z+0.2x \: [m/s]$](img35.gif) . For this case I use a PSPI and a
Split-Step datuming algorithm. The last velocity model
consists of three vertical areas of constant velocity
. For this case I use a PSPI and a
Split-Step datuming algorithm. The last velocity model
consists of three vertical areas of constant velocity
![$v(x)=(1000.,2000.,3000.) \: [m/s]$](img36.gif) .
.
All the conjugate operators used in this paper (Gazdag migration
and modeling, Gazdag datuming, PSPI migration and modeling,
PSPI datuming, Split-Step migration and modeling, Split-Step datuming)
pass the Dot-Product test.
data3datum
Figure 4 Effect on initial data of the datuming algorithm (constant velocity).
a. Initial data at the flat surface.
b. Data on the topographic datum.
c. Data after datuming to the topographic surface and back.




 Mig2Datum
Mig2Datum
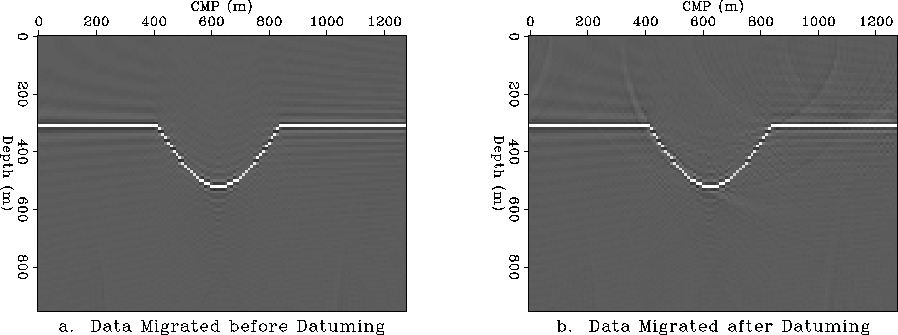
Figure 5 Migration before and after datuming in constant velocity.
a. Migration before datuming.
b. Migration after continuing the wavefield to the topographic
surface and back to the flat datum.




 data3datumvz
data3datumvz
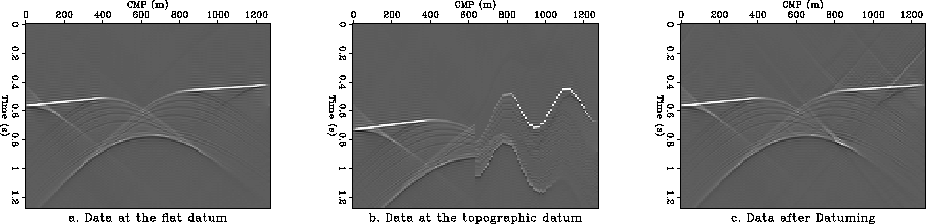
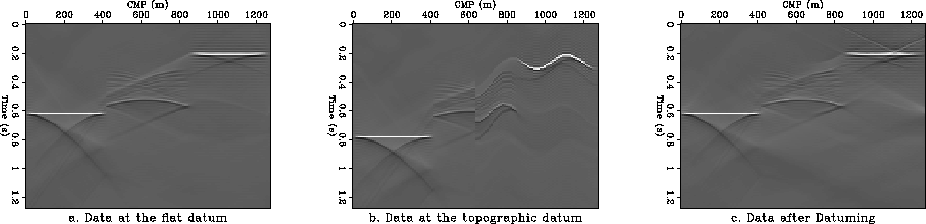
Figure 6 Effect on initial data of the datuming algorithm v(z)=1000+0.6*z.
a. Initial data at the flat surface.
b. Data on the topographic datum.
c. Data after datuming to the topographic surface and back.




 Mig2Datumvz
Mig2Datumvz
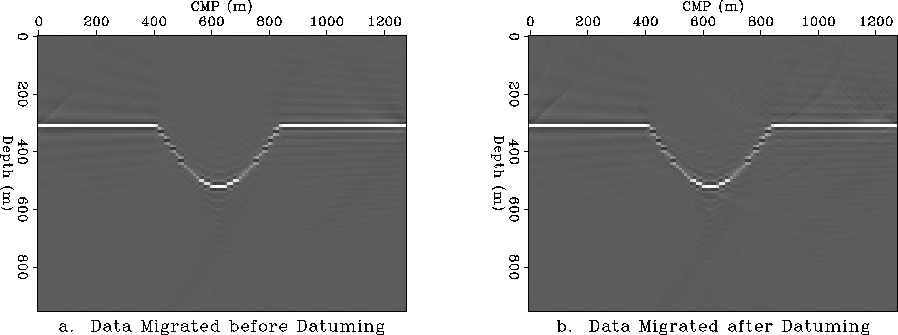
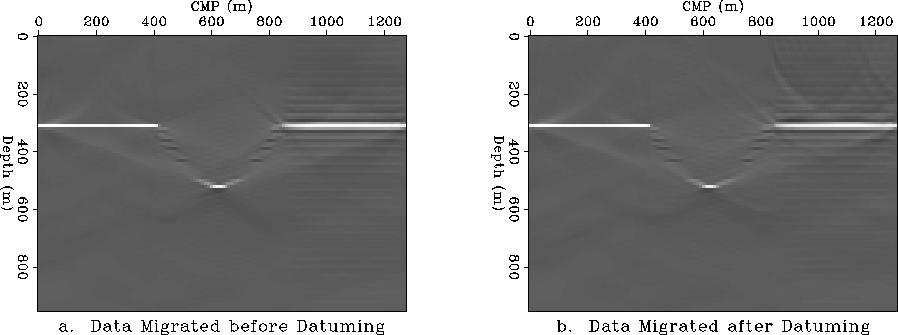
Figure 7 Migration before and after datuming in depth variable velocity v(z).
a. Migration before datuming.
b. Migration after continuing the wavefield to the topographic
surface and back to the flat datum.




 data3datumsplit
data3datumsplit
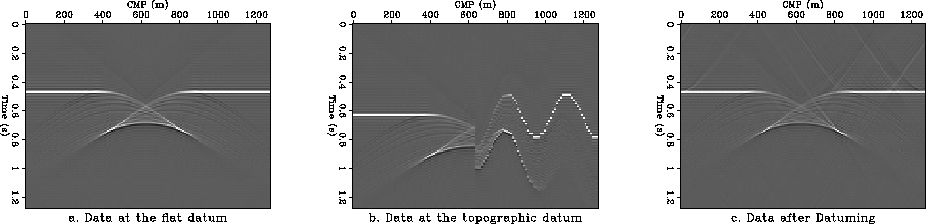
Figure 8 Effect on initial data of the datuming algorithm v(x,z).
Split-Step.
a. Initial data at the flat surface.
b. Data on the topographic datum.
c. Data after datuming to the topographic surface and back.




 Mig2Datumsplit
Mig2Datumsplit
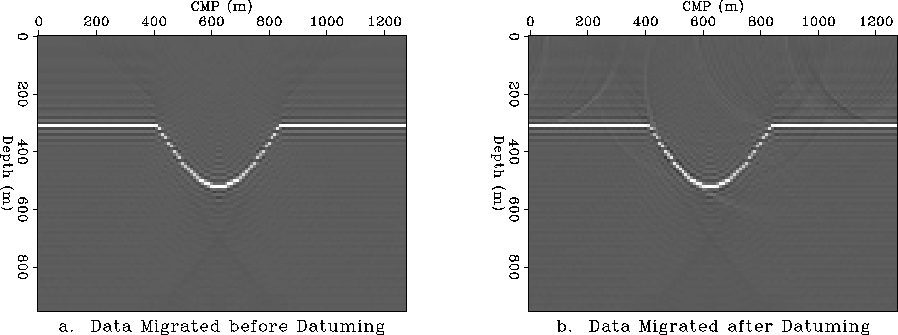
Figure 9 Migration before and after datuming. v(x,z)=v0+ax*x+az*z.
a. Migration before datuming (Split-Step).
b. Migration after continuing the wavefield to the topographic
surface and back to the flat datum (Split-Step).




 data3datumpspi
data3datumpspi
Figure 10 Effect on initial data of the datuming algorithm v(x,z).
PSPI datuming.
a. Initial data at the flat surface.
b. Data on the topographic datum.
c. Data after datuming to the topographic surface and back.




 Mig2Datumpspi
Mig2Datumpspi
Figure 11 Migration before and after datuming.
v(x,z)=v0+ax*x+az*z.
a. Migration before datuming (PSPI).
b. Migration after continuing the wavefield to the topographic
surface and back to the flat datum (PSPI).




 data3datumxsplit
data3datumxsplit
Figure 12 Effect on initial data of the datuming algorithm v(x,z).
Split-Step.
a. Initial data at the flat surface.
b. Data on the topographic datum.
c. Data after datuming to the topographic surface and back.




 Mig2Datumxsplit
Mig2Datumxsplit
Figure 13 Migration before and after datuming in
v(x,z)=1000,2000,3000 velocity.
a. Migration before datuming (Split-Step).
b. Migration after continuing the wavefield to the topographic
surface and back to the flat datum (Split-Step).




 data3datumxpspi
data3datumxpspi
Figure 14 Effect on initial data of the datuming algorithm v(x,z).
PSPI datuming.
a. Initial data at the flat surface.
b. Data on the topographic datum.
c. Data after datuming to the topographic surface and back.




 Mig2Datumxpspi
Mig2Datumxpspi
Figure 15 Migration before and after datuming in
v(x,z)=1000,2000,3000 velocity.
a. Migration before datuming (PSPI).
b. Migration after continuing the wavefield to the topographic
surface and back to the flat datum (PSPI).










Next: Future work
Up: WAVE-EQUATION DATUMING ALGORITHM
Previous: Wave-equation Datuming for laterally
Stanford Exploration Project
11/17/1997

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The reflectivity model consists of a syncline in the middle of a horizontal layer.
In order to analyze how the datuming algorithm affects
the initial data I apply the conjugate pair of datuming operators and
compare the resulting data with the initial data.
.
The reflectivity model consists of a syncline in the middle of a horizontal layer.
In order to analyze how the datuming algorithm affects
the initial data I apply the conjugate pair of datuming operators and
compare the resulting data with the initial data.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows an example for a constant velocity medium.
The zero-offset data is then extrapolated to the uneven topographic datum
shown in Figure
a shows an example for a constant velocity medium.
The zero-offset data is then extrapolated to the uneven topographic datum
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to obtain the data in Figure
to obtain the data in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
Using the conjugate transpose algorithm, data is extrapolated back
to the flat datum to obtain the third panel in Figure
b.
Using the conjugate transpose algorithm, data is extrapolated back
to the flat datum to obtain the third panel in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c.
By comparing the first and the third panel in Figure
c.
By comparing the first and the third panel in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we
can estimate the effect of the datuming algorithm on the initial data.
we
can estimate the effect of the datuming algorithm on the initial data.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a and then again after the pair of
conjugate datuming operators is applied. The migrated image
after conjugate datuming is shown in Figure
a and then again after the pair of
conjugate datuming operators is applied. The migrated image
after conjugate datuming is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
b.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
is just constant. The next model, used to obtain Figures
,
is just constant. The next model, used to obtain Figures
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , is a linearly increasing
velocity in depth
, is a linearly increasing
velocity in depth ![]() . The third velocity model
is linearly increasing both in depth and laterally
. The third velocity model
is linearly increasing both in depth and laterally
![]() . For this case I use a PSPI and a
Split-Step datuming algorithm. The last velocity model
consists of three vertical areas of constant velocity
. For this case I use a PSPI and a
Split-Step datuming algorithm. The last velocity model
consists of three vertical areas of constant velocity
![]() .
.