Approximating TI dispersion relations

Now that we have related transverse isotropy to our anelliptic approximations we show an example of using these approximations to do Fourier-domain migration. (For a real data example using the first anelliptic approximation for Fourier-domain imaging see Gonzalez et al. (1991).)

Figure  shows the result of diffracting, then migrating, a model consisting of five point diffractors arranged in a diamond. Scalar Stolt diffraction and time-migration with an anisotropic dispersion relation were used to do the calculations; the dispersion relation is for the qP (left column) and qSV (right column) wavetypes of the TI medium Greenhorn Shale (Jones and Wang, 1981). The result is not perfect because of the offset truncation of the modeled hyperboloids. The right-hand depth scale on the time migrations uses the true vertical velocities to convert from time to depth.

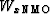Figure  shows the results of time-migrating the modeled qP and qSV hyperboloids from Figure  using isotropic dispersion relations. The velocities used are the usual ones determined from moveout, $W_{x{\mbox{\rm\scriptsize NMO}}}$.Even for the less extreme qP wavetype (left column) the isotropic migration manages to properly focus only the nearest-offset part of the hyperboloids.

There is a more subtle error in the isotropic migration as well. The true vertical scale cannot be determined from surface data alone, but isotropy makes no allowance for this ambiguity and just assumes the vertical velocity is the same as the moveout velocity. As a result, the right-hand depth scale for the qSV waves is off by nearly a factor of two. (The depth scale for the qP waves also mislocates the diffractors, but only by about 5%.)

Figure  shows the results of using the first anelliptic approximation to time-migrate the modeled TI hyperboloids in Figure . The approximation is meant to be fit using only surface data, so as in Figure  the unknowable vertical velocity has been set equal to the moveout velocity. Unlike the isotropic approximation in Figure , though, the first anelliptic approximation does a good job of focusing the hyperboloids, especially for the less extreme qP wavetype.

In Figure  we improve the fit to the second anelliptic approximation. The main difference is that the qSV diffractors are better focused. Since fitting the second anelliptic approximation assumes access to horizontal as well as vertical data, the correct vertical velocity has been used and the right-hand depth scales are correct.