




Next: RESULTS
Up: Karrenbach, Nichols & Muir:
Previous: FINITE DIFFERENCE METHOD
Reflection amplitudes at the interface are retrieved by operating in the
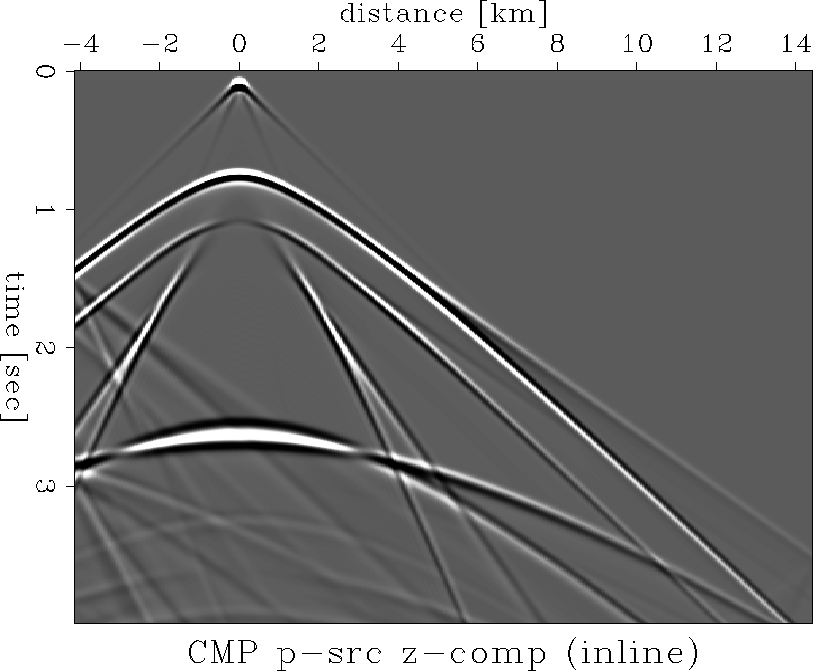
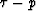 domain. Looking at the recorded time domain CMP records (
Figures
domain. Looking at the recorded time domain CMP records (
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we
see an amplitude estimation problem near 1.75 sec
caused by triplicating branches of reflection hyperbolae.
Transforming those records to the
) we
see an amplitude estimation problem near 1.75 sec
caused by triplicating branches of reflection hyperbolae.
Transforming those records to the 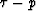 domain
gets rid of triplications and provides a
robust estimate of the ``phase domain'' representation of the
reflected waves in an anisotropic medium. Thus the traveltime curves
in the
domain
gets rid of triplications and provides a
robust estimate of the ``phase domain'' representation of the
reflected waves in an anisotropic medium. Thus the traveltime curves
in the 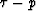 domain are simple curves. From a practical point of view
the slant-stack domain offers more advantages such as, dealiasing
Nichols (1992), aperture and geometry compensated estimates of
the wave field Kostov (1990), and regridding (inteerpolation) capabilities.
The events of interest in Figures
domain are simple curves. From a practical point of view
the slant-stack domain offers more advantages such as, dealiasing
Nichols (1992), aperture and geometry compensated estimates of
the wave field Kostov (1990), and regridding (inteerpolation) capabilities.
The events of interest in Figures
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (inline)
are the
uppermost two elliptical curves corresponding to the PP and PS reflection
from the shale/chalk interface.
The slant-stack difference sections, obtained by subtracting the
crossline slant-stack section from the inline counterpart
gives Figure
(inline)
are the
uppermost two elliptical curves corresponding to the PP and PS reflection
from the shale/chalk interface.
The slant-stack difference sections, obtained by subtracting the
crossline slant-stack section from the inline counterpart
gives Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The differences are obvious at values close to critical horizontal slowness,
and at the triplicating event for a large array of horizontal
slowness values.
.
The differences are obvious at values close to critical horizontal slowness,
and at the triplicating event for a large array of horizontal
slowness values.
The first step in amplitude extraction is to transform the CMP
gathers into the  -p space using an ``optimum''
least-squares procedure,
aiming to give us an unbiased, amplitude preserving estimate of the wave field.
The traveltimes in the slant-stack domain are skewed ellipses in the
anisotropic case. Since we are interested in PP and PS reflection, it is
useful to write the Double Square Root (DSR) equation in the
-p space using an ``optimum''
least-squares procedure,
aiming to give us an unbiased, amplitude preserving estimate of the wave field.
The traveltimes in the slant-stack domain are skewed ellipses in the
anisotropic case. Since we are interested in PP and PS reflection, it is
useful to write the Double Square Root (DSR) equation in the  -p domain.
The DSR equation
-p domain.
The DSR equation
| 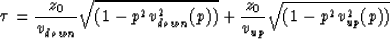 |
(1) |
is a sum of two skewed square roots. Here the velocity depends on the
ray parameter, but may not vary laterally. If vdown is not
identical to vup, we are calculating the traveltime for a
mode-converted wave. Amplitudes can then be extracted along a
prescribed corridor given by the  -p traveltime curve in
conjunction with the dominant wavelet period. From those extracted values the
amplitude at the centroid frequency is picked. This gives us a robust
reflection energy estimate for a given definite wave type.
pxseis.f10.0.cmp.SUB
-p traveltime curve in
conjunction with the dominant wavelet period. From those extracted values the
amplitude at the centroid frequency is picked. This gives us a robust
reflection energy estimate for a given definite wave type.
pxseis.f10.0.cmp.SUB
Figure 5 Recorded seismograms from a p-source into an x-component.
 pzseis.f10.0.cmp.SUB
pzseis.f10.0.cmp.SUB
Figure 6 Recorded seismogram from a p-source into an x-component.
 pxseis.f10.0.cmp.SUB.SL
pxseis.f10.0.cmp.SUB.SL
Figure 7 The CMP gather (Fig. ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is transformed using a least-squares slant-stack.
) is transformed using a least-squares slant-stack.
 pzseis.f10.0.cmp.SUB.SL
pzseis.f10.0.cmp.SUB.SL
Figure 8 The CMP gather (Fig. ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is transformed using a least-squares slant-stack.
) is transformed using a least-squares slant-stack.
 pxseis.f10.SL.DIFF
pxseis.f10.SL.DIFF
Figure 9 Subtraction of inline and crossline slant-stacks.
 pzseis.f10.SL.DIFF
pzseis.f10.SL.DIFF
Figure 10 Subtraction of inline and crossline slant-stacks.






Next: RESULTS
Up: Karrenbach, Nichols & Muir:
Previous: FINITE DIFFERENCE METHOD
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we
see an amplitude estimation problem near 1.75 sec
caused by triplicating branches of reflection hyperbolae.
Transforming those records to the
) we
see an amplitude estimation problem near 1.75 sec
caused by triplicating branches of reflection hyperbolae.
Transforming those records to the ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (inline)
are the
uppermost two elliptical curves corresponding to the PP and PS reflection
from the shale/chalk interface.
The slant-stack difference sections, obtained by subtracting the
crossline slant-stack section from the inline counterpart
gives Figure
(inline)
are the
uppermost two elliptical curves corresponding to the PP and PS reflection
from the shale/chalk interface.
The slant-stack difference sections, obtained by subtracting the
crossline slant-stack section from the inline counterpart
gives Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The differences are obvious at values close to critical horizontal slowness,
and at the triplicating event for a large array of horizontal
slowness values.
.
The differences are obvious at values close to critical horizontal slowness,
and at the triplicating event for a large array of horizontal
slowness values.
![]() -p space using an ``optimum''
least-squares procedure,
aiming to give us an unbiased, amplitude preserving estimate of the wave field.
The traveltimes in the slant-stack domain are skewed ellipses in the
anisotropic case. Since we are interested in PP and PS reflection, it is
useful to write the Double Square Root (DSR) equation in the
-p space using an ``optimum''
least-squares procedure,
aiming to give us an unbiased, amplitude preserving estimate of the wave field.
The traveltimes in the slant-stack domain are skewed ellipses in the
anisotropic case. Since we are interested in PP and PS reflection, it is
useful to write the Double Square Root (DSR) equation in the ![]() -p domain.
The DSR equation
-p domain.
The DSR equation
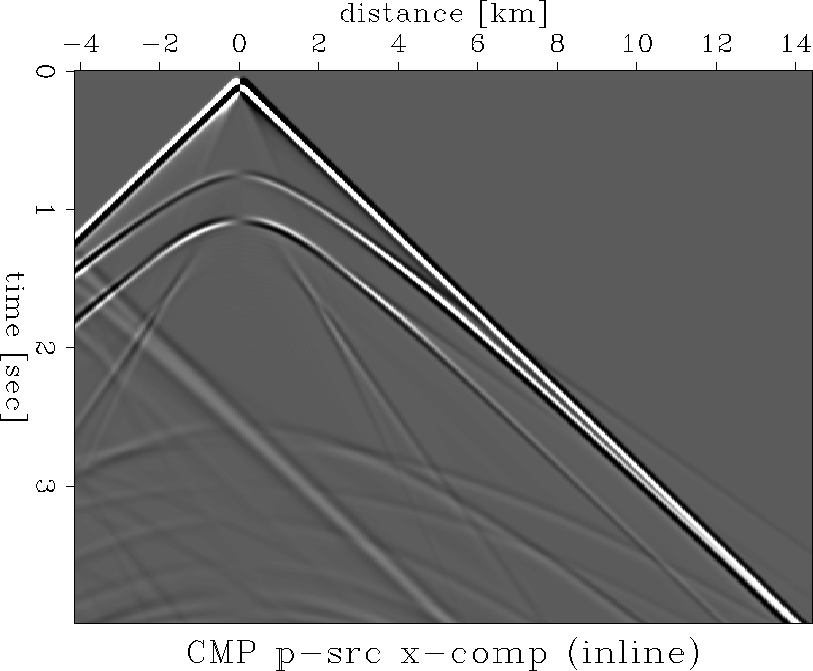

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is transformed using a least-squares slant-stack.
) is transformed using a least-squares slant-stack.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is transformed using a least-squares slant-stack.
) is transformed using a least-squares slant-stack.

