In addition to the basic ![]() and
and ![]() classes,
there are also classes that define arrays of each. A
``
classes,
there are also classes that define arrays of each. A
``![]() '' is a two dimensional array of
'' is a two dimensional array of ![]() , which are
not necessarily conformable with each other. An operator array is also
a two dimensional array which contains operators. Applying a
, which are
not necessarily conformable with each other. An operator array is also
a two dimensional array which contains operators. Applying a ![]() to a
to a ![]() :
:
![]()
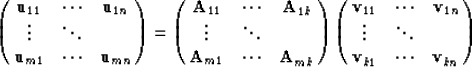
In C++, this looks like:
<type>spacearray u = B.Forward(v);This is almost identical to the syntax for applying a single operator to a single space, except here the variables u and v are of class
A simple example of using arrays is to generate a damped operator from the regular operator. If we wish to calculate the damped solution to the problem
![]()
| |
(1) |
The new operator, ![]() can be written
as
can be written
as
![]()
![]()
![]()
The following routine gives the damped least squares solution to
any linear problem that can be posed in terms of opa,
an instance of the class ![]() ,and a RHS, y, of the class
,and a RHS, y, of the class ![]() .
.
// This routine gives a damped solution to the least squares problem
// opa.Forward( x ) = y;
// by augmenting the operator with a diagonal damping matrix
<type>space damped_solver( <type>space& x0, // initial solution
<type>op opa, // linear operator
<type>space& y, // rhs
float epsilon, // the damping factor
int maxiter ) // maximum no. of iterations
{
<type>oparray ops(2); // declare a 2x1 operator array
<type>Scale scale( epsilon ); // scale is a diagonal scaling operator
ops(1) = &opa; ops(2) = &scale; // assign the elements of the operator array
<type>spacearray rhs(2) // declare a 2x1 rhs array of spaces.
<type>space zero = x.empty() // zero is the same shape as x but all zeros.
rhs(1) = y; rhs(2)=zero // assign the elements of the rhs
// now solve the augmented problem, and return the result
return <type>space soln = <type>arraysolver( x0, ops, rhs, maxiter );
}
The new operator ops ( of class