An alternate approach - plane fitting

Spatial prediction gives us the coherence as a function of apparent dip, measured along a number of azimuths. As an alternative to the dip scanning method used above, we could pick the best apparent dip for each trace pair, and then from these many apparent dips, select one (or more) true dips for interpolation. For example, we could fit a single plane to all the apparent dip measurements using least-squares. The overdetermined problem looks like this:

 

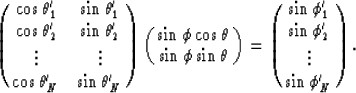
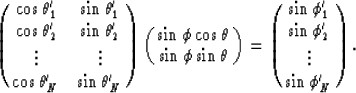$$\pmatrix{\cos \theta_1'&\sin \theta_1'\cr \cos \theta_2'&\s... ...rix{\sin \phi_1'\cr \sin \phi_2'\cr \vdots\cr \sin \phi_N'}.$$ (2)

Here the unknows are $\phi$ and $\theta$, the dip and azimuth angles of the true dip, the plane we are fitting to the data. The known $\phi_i'$ and $\theta_i'$ are the measured apparent dips and the azimuth angles along which they are measured.

In the presence of a single dip, this method works well, and is significantly less costly than a global search of the dip space. In the presence of multiple dips, however, the least-squares technique will choose an intermediate dip to minimize the error, a dip which may not interpolate any of the dips particularly well. The dip-scanning method presented above will at least interpolate one dip, that which gives the best coherence, well.

The best solution to the case of conflicting dips may be a plane-fitting approach that fits multiple planes to the set of apparent dip measurements. Fitting multiple planes is significantly more difficult than fitting a single plane. Possibly an L1-norm scheme could help.