CONCLUSIONS

A tomographic inversion technique that fits seismic traveltimes with elliptical velocity functions has been presented. The elliptical parameters estimated with this inversion can be inserted into the double elliptic approximation to estimate more general transversely isotropic models, when data from different geometries is used.

Since the inclination of the axis of symmetry is also a variable in the inversion procedure, certain types of azimuthally anisotropic media can be approximated, in particular those formed by dipping transversely isotropic layers.

 

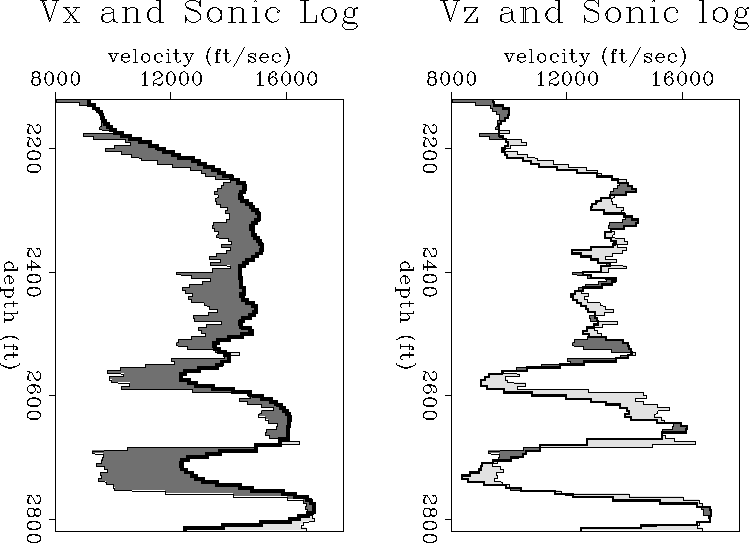
devine-log-vel
Figure 10 Result of the inversion. An average sonic log (thinner curve) blocked every 7 ft is compared with the two estimated velocities. The vertical velocity is closer and better correlated to the log. Notice how the amount of anisotropy changes through the model, reaching a peak at the shale and clay intervals. The model is described by 128 layers.

The model for heterogeneities is described as a superposition of homogeneous orthogonal regions whose boundaries may change their positions as iterations proceed but are not allowed to cross in the area of interest. When two parallel interfaces move too close to each other, one of them (along with its upper interval) is eliminated from the inversion, reducing the number of unknowns. The technique was successfully applied to synthetic and field data where both strong anisotropy and strong velocity contrasts were present.