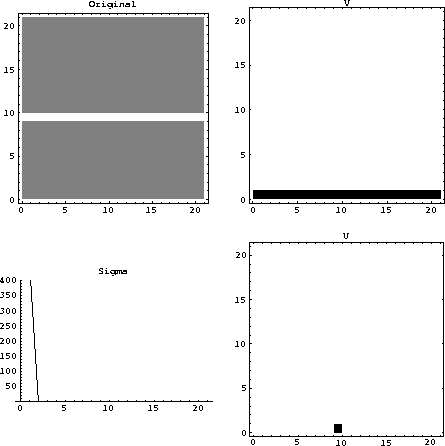Compared to photographs, reflection seismic datasets are poorly compressed with the singular value decomposition. Dipping events extend the range of singular values that contain significant energy, invalidating the assumption that only the small singular values are needed to reconstruct the image. Fine detail, including noise, tends to be associated with the small singular values and is lost using reconstructions with only the large singular values.
Dipping events do not fall along columns or rows of the original image and are spread over a wide range of singular values, violating the assumption that we can represent the input with only the first few singular values. Examples shown in Figures 3 to 5 show the number of significant singular values increases with dip. Figure 3 shows a flat event and its decomposition. This event has only one significant singular value and can be reconstructed with a single row of V and a single column of U. If a dipping event is decomposed as seen in Figure 4, the number of singular values increases and the amount of data needed to reconstruct the image is larger than that needed to reconstruct the image of the flat event. If an event with even more dip is decomposed as seen in Figure 5, all the singular values must be used to reconstruct the image, and the amount of data needed to store the U and V matrices is greater than the size of the original image.
|
flat
Figure 3 A flat event and its decomposition. Notice that there is only one nonzero singular value. |  |
|
dip
Figure 4 A dipping event and its decomposition. Notice that there are now many more nonzero singular values. |  |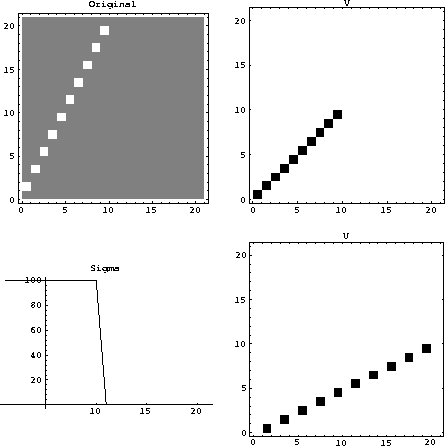
|
diag
Figure 5 An even steeper dipping event and its decomposition. Every singular value is now equal. |  |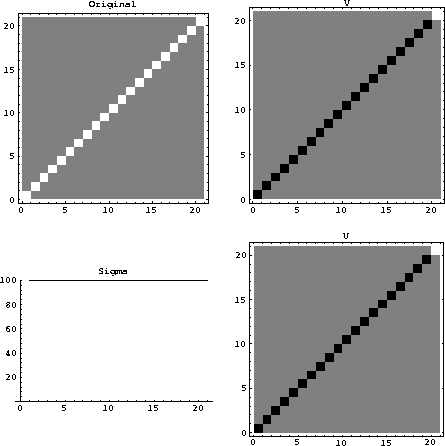
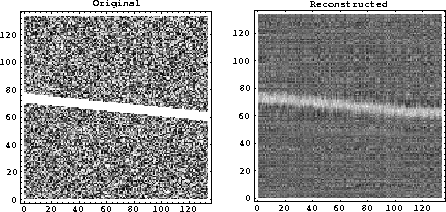
High frequency events in time and space containing the fine detail of an image tend to be distributed in the partial images corresponding to small singular values. The decomposition of the photograph shown in Figure 1 shows high frequency events in the upper rows of the U and V matrices that correspond to the smaller singular values. In photographs like Figure 1, much of the image is made up of large uniform areas; in contrast, seismic images contain mainly fine detail. Figure 6 shows the decomposition of a dipping event in a background of random numbers that simulates a seismic file with one strong event and much small detail. If the U and V matrices are examined carefully, low frequency signals corresponding to the dipping event are seen in the bottom few rows. When the image is reconstructed in Figure 7 with a few large singular values, the background shows a loss of random noise. Even worse, the strong event is corrupted with noise from outside the event, and the random noise is organized along the columns and rows.
 |
 |
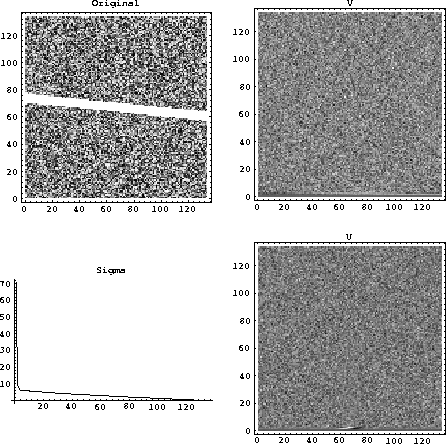