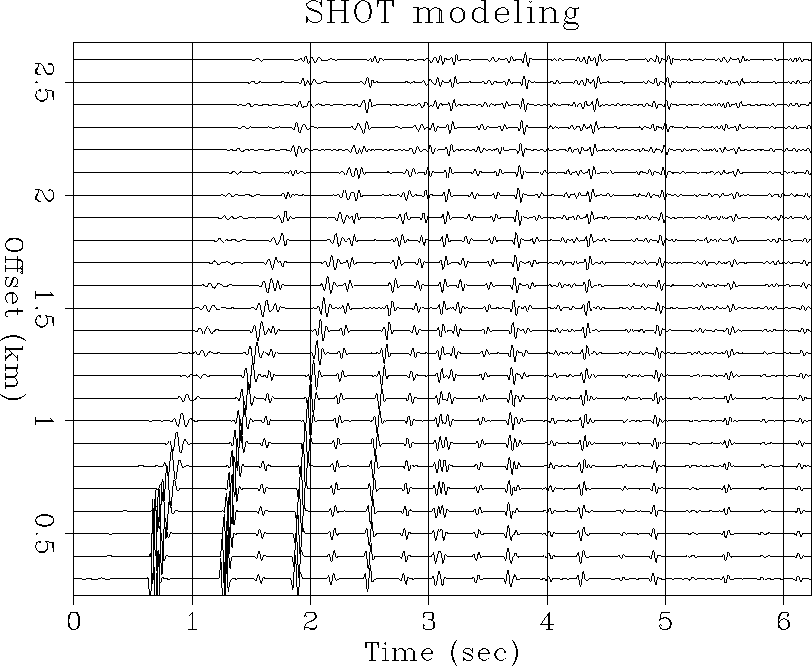
 |
Figure 1 Synthetic data with water-related reverberations.
At this stage, we implement only the first two attributes, (g1=T, g2=T.Vnmo2). The addability of T and T.Vnmo2 means that waterbottom multiples and peglegs lie evenly sampled along each of these two axes. Then they lie evenly sampled along parallel lines in the (g1,g2) plane, the slope being the water velocity squared. Figure 1 is a Solid elastic modeling dataset that has geology similar to that of the Geco Barents Sea dataset we will study later.
 |
We apply velocity transform by NMO Kirchhoff summation on this dataset into the zero-offset two way travel time and slowness squared domain (T,1/Vnmo2) (Claerbout, 1992). The zero-offset travel time is already an Abelian group, g1=T. We apply a shear by nearest neighbor interpolation along the slowness squared axis to transform into the Dix's parameter, g2=T.Vnmo2. The results are shown in Figure 2, where the waterbottom multiples and peglegs lie evenly spaced along parallel straight lines in the Abelian group plane. The events in the velocity space span a large area because of the insensitivity of velocity transformation.
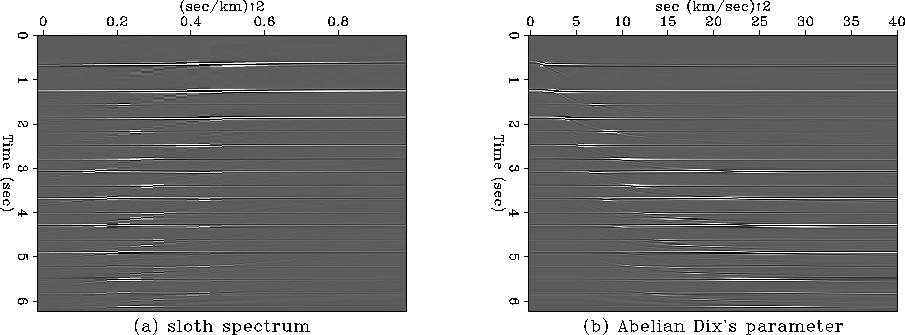 |
The next most important property of the Abelian group is closure. Closure means that any linear combination of different Abelian group attributes also forms an Abelian group. If we have a set of vectors v, which forms such a group, then for any constant matrix, M, the set of vectors M.v, also forms such a group. We introduce a shear into the (g1,g2) coordinate frame in Figure 2 by replacing (T.Vnmo2) with the linear combination (T.Vnmo2 - T.Vwater2) since we are concerned with the water-bottom multiples and their peglegs (or some other lower-bounding velocity if other intrabed multiples are concerned). The slope of the waterbottom multiples and peglegs - Vwater2 in (g1,g2) plane can either be known from field water velocity measurement or from looking at the Hilbert envelope of the data, and then finding the shear on the data (i. e., by varying Vwater2) that maximizes the sum of the envelope energy over axis T. Then the waterbottom multiples and peglegs are steered straight down the T axis. Thus in this domain, predictive multiple attenuation operators will work well. This process yields the new Abelian group attributes: