More DMO kinematics

We defined DMO as an operator which together with NMO transforms data from constant-offset to zero offset. After Zero-Offset Migration (ZOM) the result of our data processing sequence is equal to the output of Prestack Migration (PsM). We can write this in a formal form

$$(NMO \cdot DMO)(ZOM)={MZO \cdot ZOM} = PsM .$$

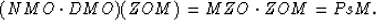
Using this definition we can describe the sequence 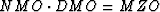$NMO \cdot DMO = MZO$ as  

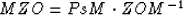$$MZO= {PsM \cdot {ZOM}^{-1}}$$ (9)

where the MZO operator can be built using the Prestack Migration operator and the inverse of the Zero-Offset Migration operator, which is the Zero-Offset Modeling.

We use this definition to define a MZO operator not only for a constant velocity medium, but for any variable velocity medium. The impulse response of the generalized 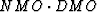$NMO \cdot DMO$can be defined by a two step process:

1.

Full prestack migration to a depth model. The prestack depth model is the position in space of all points that can generate a given impulse in a constant-offset section. For a constant velocity medium this is equivalent to constructing the migration ellipse for a constant-offset section. For a variable velocity medium, the loci of points with equal travel-time from source to receiver form a curve resembling an ellipse or a superposition of several ellipses.

2.

Zero-offset modeling. Given the depth model, raytrace back at 90 degrees from the reflector, to model the zero-offset data. The intersection of the ray with the surface will give the x-coordinate of the MZO operator, while the travel-time along the raypath will provide the zero-offset time-coordinate.

Using this definition we can find another path to derive analytically the DMO operator in constant velocity media.