




Next: An alternative method
Up: SOLUTIONS
Previous: SOLUTIONS
A straightforward solution to (1) is trace interpolation.
But because of the very simple form of stretch, there are elegant
alternatives to explicit trace interpolation.
After logarithmic and Fourier transformation of the time function p(t)
the original stretch can be performed by a simple multiplication![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
:
| 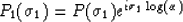 |
(2) |
For brevity, we will refer to this 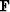 ourier transformed
ourier transformed 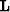 ogarithmic domain
as
ogarithmic domain
as 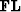 domain.
domain.
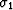 denotes the variable in the
denotes the variable in the 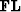 domain after stretching.
domain after stretching.
To prevent the time trace from being undersampled, the trace after
logarithmic transformation will have to have ns samples![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) , where
, where
| 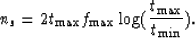 |
(3) |
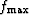 is the maximum frequency of p(t),
is the maximum frequency of p(t),
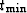 ,
, 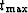 are the upper and lower limits of the section of
p(t), that
the logarithmic trace of ns points resamples
correctly. In practice the logarithmic trace is often found to be
extremely long.
are the upper and lower limits of the section of
p(t), that
the logarithmic trace of ns points resamples
correctly. In practice the logarithmic trace is often found to be
extremely long.





Next: An alternative method
Up: SOLUTIONS
Previous: SOLUTIONS
Stanford Exploration Project
11/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
:
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) :
:
![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) , where
, where