Next: Wave field types
Up: Karrenbach: source equalization
Previous: Introduction
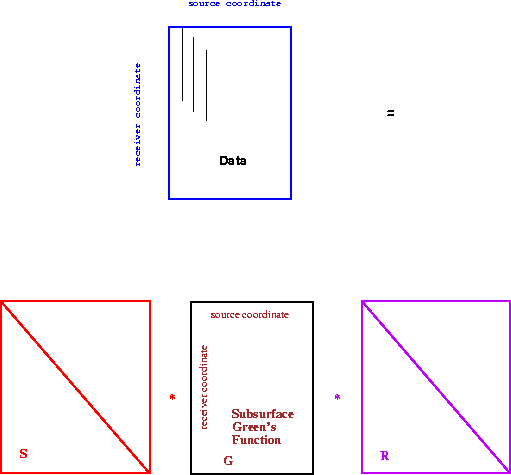
I am using the basic notion of symmetry in a wave field, or to be more precise
the lack thereof. To expand that idea, let us look at a single
slice through a prestack data volume. Let the data depend on the
following variables:
| 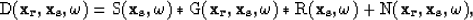 |
(1) |
where 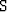 describes the source behavior,
describes the source behavior, 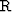 describes the receiver behavior,
and
describes the receiver behavior,
and 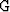 governs pure propagation effects through the medium.
governs pure propagation effects through the medium.
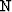 is an additive noise term.
In an ideal world
is an additive noise term.
In an ideal world 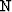 would be zero, as in Figure
would be zero, as in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
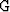 represents the Green's function of the
medium. It can be shown that
since the anisotropic elastic wave equation is linear and self-adjoint,
the discrete representation
of the continuous function
represents the Green's function of the
medium. It can be shown that
since the anisotropic elastic wave equation is linear and self-adjoint,
the discrete representation
of the continuous function 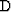 has to be symmetric.
That is,
has to be symmetric.
That is,
| 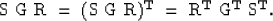 |
(2) |
This equation defines a measure for the symmetry of a given data set.
The symmetric part of data is defined as
| 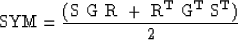 |
(3) |
and the antisymmetric part of the data as
| 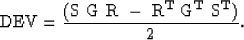 |
(4) |
matrix
Figure 1 Schematic representation of a discrete
symmetric wave field






Next: Wave field types
Up: Karrenbach: source equalization
Previous: Introduction
Stanford Exploration Project
11/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.