




Next: The predictability of linear
Up: THE LINEAR TWO-STEP METHOD
Previous: THE LINEAR TWO-STEP METHOD
A seismic event is called a linear event if it follows a linear trajectory.
Usually such an event is mathematically described as:
w(t-px),
where w is the wavelet of the event, and p is the dip of the event.
This description implies that the amplitudes of the wavelets are constant
along the event. However field data show that wavelets along seismic events
have slowly varying amplitude. Therefore, without loss of generality, we
can describe a linear event by allowing its amplitude to vary exponentially
as follows:
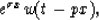
where  is limited to being a real number that determines
the rate of amplitude variation. An event with a complicated
amplitude function is represented as a superposition of multiple
linear events with the same dip. Since these amplitude variations are
usually smooth, we expect that the magnitude of
is limited to being a real number that determines
the rate of amplitude variation. An event with a complicated
amplitude function is represented as a superposition of multiple
linear events with the same dip. Since these amplitude variations are
usually smooth, we expect that the magnitude of  is small, and that
the amplitude functions can be represented by a few exponential functions.
is small, and that
the amplitude functions can be represented by a few exponential functions.





Next: The predictability of linear
Up: THE LINEAR TWO-STEP METHOD
Previous: THE LINEAR TWO-STEP METHOD
Stanford Exploration Project
11/18/1997
![]()