




Next: False start
Up: Claerbout: LOcal MOnoPLane ANnihilator
Previous: FIELD DATA TESTS
We seek the general form of a filter
to apply to a data cube 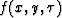 that will annihilate a plane function
that will annihilate a plane function
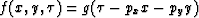 where g() is
an arbitrary one-dimensional function.
In practice we usually need to allow the filter to vary with
where g() is
an arbitrary one-dimensional function.
In practice we usually need to allow the filter to vary with 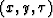 ,but first we investigate the constant dip case.
For warmup we consider the case when
,but first we investigate the constant dip case.
For warmup we consider the case when 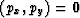 and later we consider nonzero values of (px,py).
Clearly we can annihilate this plane with either
the operator
and later we consider nonzero values of (px,py).
Clearly we can annihilate this plane with either
the operator 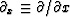 or the operator
or the operator 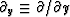 .The problem with the operator
.The problem with the operator 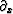 is that it annihilates not only the vertical plane function
is that it annihilates not only the vertical plane function 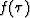 but it annihilates other things such as functions of the form
but it annihilates other things such as functions of the form 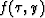 ,an example of which is the family of planes,
,an example of which is the family of planes, 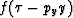 .A way to annihilate one plane and only one plane is
to choose a filter with
two outputs,
namely the filter
.A way to annihilate one plane and only one plane is
to choose a filter with
two outputs,
namely the filter 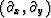 .For this two-component output to be annihilated
in a regression,
both components must be annihilated.
This is the lowest order filter that will do the required job.
We can make a higher order filter
that annihilates the plane by multiplying the column vector filter
.For this two-component output to be annihilated
in a regression,
both components must be annihilated.
This is the lowest order filter that will do the required job.
We can make a higher order filter
that annihilates the plane by multiplying the column vector filter
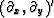 by its conjugate getting the negative of the Laplacian
by its conjugate getting the negative of the Laplacian
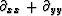 .An apparent advantage of the Laplacian filter
is that its output is a single volume.
In time we will learn the practical distinction between
these two monoplane annihilators.
For now, I am betting on the two-output lower order filter.
.An apparent advantage of the Laplacian filter
is that its output is a single volume.
In time we will learn the practical distinction between
these two monoplane annihilators.
For now, I am betting on the two-output lower order filter.





Next: False start
Up: Claerbout: LOcal MOnoPLane ANnihilator
Previous: FIELD DATA TESTS
Stanford Exploration Project
11/18/1997