Next: CONCLUSIONS
Up: Biondi: Solving the frequency-dependent
Previous: Evaluation of derivatives of
To test the accuracy of the proposed solution of
the frequency-dependent eikonal equation
I compared results obtained by extrapolating the
phase slowness with
the results obtained from a
wave-equation modeling by finite differences.
I used two simple models for this testing.
Both models present a Gaussian-shaped circular velocity
anomaly in a constant velocity background,
in the first example the perturbation is negative,
in the second one it is positive.
I chose anomalies of opposite signs because I wanted
to test the accuracy of my method both in presence
of focusing of the wavefield (negative perturbation) and of defocusing
(positive perturbation).
In the first example the background velocity is 3 km/s,
the maximum amplitude of the anomaly is 1.5 km/s and
its width is about 100 m.
I started the extrapolation process at infinite frequency
and stopped when it reached the frequency of 5 Hz.
The extrapolation step was constant in inverse frequency  .Figure
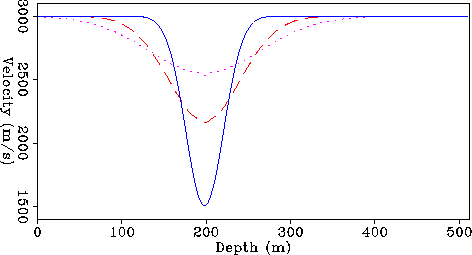
.Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a vertical slice of the resulting
velocity model for three different frequencies.
The solid line shows the medium slowness; that is, the infinite frequency
slowness. The dashed line shows the phase slowness
at 12.5 Hz, corresponding to a wavelength of 240 m.
Finally the dotted line shows the phase slowness at
5 Hz, corresponding to a wavelength of 600 m.
As frequency decreases,
the frequency extrapolation progressively smooths the slowness
model.
shows a vertical slice of the resulting
velocity model for three different frequencies.
The solid line shows the medium slowness; that is, the infinite frequency
slowness. The dashed line shows the phase slowness
at 12.5 Hz, corresponding to a wavelength of 240 m.
Finally the dotted line shows the phase slowness at
5 Hz, corresponding to a wavelength of 600 m.
As frequency decreases,
the frequency extrapolation progressively smooths the slowness
model.
Velneg
Figure 1 A vertical slice of the phase-slowness function for three
different frequencies:
infinite frequency (solid line),
12 Hz (dashed line), and 5 Hz (dotted line).

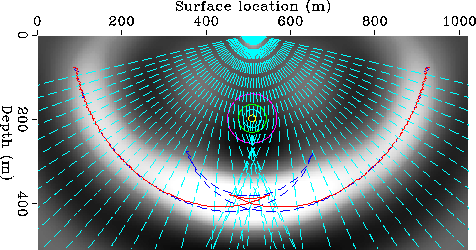
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the results
of wave-equation modeling and standard raytracing through the model.
Plots of
the rays (dashed lines)
and
the wavefront predicted by raytracing
(solid black line)
are superimposed onto a snapshot of the wavefield.
The Figure also shows a contour plot of the velocity anomaly
(white circles).
For the wave-equation modeling I used a wavelet
with central frequency of 60 Hz,
corresponding to a wavelength of 50 m.
This wavelength is
sufficiently short, compared to the the width of the
anomaly, for the eikonal to correctly predict
the behavior of the wavefield.
Just beneath the peak of the anomaly,
the rays go through a caustic
and the wavefront triplicates.
The raytracing predicts
correctly the positions and amplitudes of the different branches
of the wavefield.
In contrast, when the central frequency of the wavelet
drops to 10 Hz (Figure
shows the results
of wave-equation modeling and standard raytracing through the model.
Plots of
the rays (dashed lines)
and
the wavefront predicted by raytracing
(solid black line)
are superimposed onto a snapshot of the wavefield.
The Figure also shows a contour plot of the velocity anomaly
(white circles).
For the wave-equation modeling I used a wavelet
with central frequency of 60 Hz,
corresponding to a wavelength of 50 m.
This wavelength is
sufficiently short, compared to the the width of the
anomaly, for the eikonal to correctly predict
the behavior of the wavefield.
Just beneath the peak of the anomaly,
the rays go through a caustic
and the wavefront triplicates.
The raytracing predicts
correctly the positions and amplitudes of the different branches
of the wavefield.
In contrast, when the central frequency of the wavelet
drops to 10 Hz (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) the
wavefront predicted by the eikonal does not
match the actual wavefront of the wavefield.
Figure
) the
wavefront predicted by the eikonal does not
match the actual wavefront of the wavefield.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of wave-equation modeling
with a 10 Hz wavelet and of raytracing through the
extrapolated phase slowness at a frequency of 10 Hz.
To facilitate the comparison,
I actually plotted both the wavefront predicted by
the phase slowness at 10 Hz (solid line) and
the wavefront predicted by the medium slowness (dashed line).
The low-frequency wavefront triplicates as well, but the inner
branches are much shorter than the branches in the high-frequency
wavefront.
At the particular time of the snapshot,
the low-frequency
rays are still focused beneath the anomaly, consistently with the
amplitudes of the actual wavefield,
while the high frequency rays
have already spread far apart.
shows the result of wave-equation modeling
with a 10 Hz wavelet and of raytracing through the
extrapolated phase slowness at a frequency of 10 Hz.
To facilitate the comparison,
I actually plotted both the wavefront predicted by
the phase slowness at 10 Hz (solid line) and
the wavefront predicted by the medium slowness (dashed line).
The low-frequency wavefront triplicates as well, but the inner
branches are much shorter than the branches in the high-frequency
wavefront.
At the particular time of the snapshot,
the low-frequency
rays are still focused beneath the anomaly, consistently with the
amplitudes of the actual wavefield,
while the high frequency rays
have already spread far apart.
Raynegvel60
Figure 2 A snapshot of the wavefield generated by a source with central
frequency of 60 Hz after propagating through the negative anomaly.
Plots of the velocity anomaly, the
rays traced through the medium slowness, and the wavefront
predicted by the rays
are superimposed
onto the wavefield.

Raynegvel10
Figure 3 A snapshot of the wavefield generated by a source with central
frequency of 10 Hz after propagating through the negative anomaly.
Plots of the velocity anomaly, the
rays traced through the 10 Hz phase slowness, and the wavefronts
predicted by the 10 Hz phase slowness (solid line)
and by the
medium slowness (dashed line)
are superimposed
onto the wavefield.
(Compare with Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)

The second example is similar to the first,
but the anomaly is positive instead of being
negative,
and thus the wavefield defocuses instead of
focusing.
The background velocity is 2 km/s,
and the maximum amplitude of the anomaly is 1.5 km/s.
I started the extrapolation process at infinite frequency,
and stopped it when it reached 5 Hz.
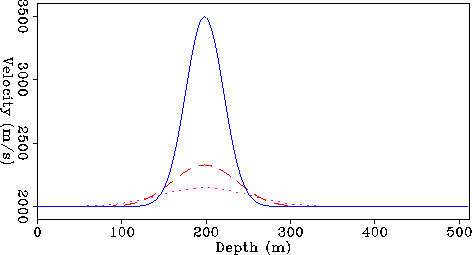
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a vertical slice of the resulting
velocity model for three different frequencies.
The solid line in the Figure shows the medium slowness.
The dashed line shows the phase slowness
at 12.5 Hz, corresponding to a wavelength of 160 m.
Finally the dotted line shows the phase slowness at
5 Hz, corresponding to a wavelength of 400 m.
Also in this case the frequency extrapolation progressively
smoothed the slowness function, but the respective
scaling of the velocity perturbations are different
from the previous example.
In this case the 12.5 Hz anomaly has a peak of about
shows a vertical slice of the resulting
velocity model for three different frequencies.
The solid line in the Figure shows the medium slowness.
The dashed line shows the phase slowness
at 12.5 Hz, corresponding to a wavelength of 160 m.
Finally the dotted line shows the phase slowness at
5 Hz, corresponding to a wavelength of 400 m.
Also in this case the frequency extrapolation progressively
smoothed the slowness function, but the respective
scaling of the velocity perturbations are different
from the previous example.
In this case the 12.5 Hz anomaly has a peak of about
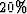 the peak of the infinite frequency slowness,
when in the previous case it was about
the peak of the infinite frequency slowness,
when in the previous case it was about 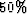 .This behavior is a clear indication that the smoothing is far
from being linear in velocity.
Although, the smoothing might be close to be linear in slowness;
this issue deserves further study.
.This behavior is a clear indication that the smoothing is far
from being linear in velocity.
Although, the smoothing might be close to be linear in slowness;
this issue deserves further study.
Velpos
Figure 4 A vertical slice of the phase-slowness function for three
different frequencies:
infinite frequency (solid line),
12 Hz (dashed line), and 5 Hz (dotted line).
(Compare with Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)

Rayposvel60
Figure 5 A snapshot of the wavefield generated by a source with central
frequency of 60 Hz after propagating through the positive anomaly.
Plots of the velocity anomaly, the
rays traced through the medium slowness, and the wavefront
predicted by the rays
are superimposed
onto the wavefield.

Rayposvel10
Figure 6 A snapshot of the wavefield generated by a source with central
frequency of 10 Hz after propagating through the positive anomaly.
Plots of the velocity anomaly, the
rays traced through the 10 Hz phase slowness, and the wavefronts
predicted by the 10 Hz phase slowness (solid line)
and by the
medium slowness (dashed line)
are superimposed
onto the wavefield.
(Compare with Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)

Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the results
of wave-equation modeling with a 60 Hz wavelet
and of raytracing through the
medium slowness.
The rays (dashed lines)
and
the wavefront predicted by raytracing
(solid black line) are
superimposed onto a snapshot of the wavefield.
The wavefield is defocused by the anomaly;
the anomaly causes
a ``shadow zone''
beneath itself,
where the amplitudes are very low.
The high-frequency rays go through a caustic
on either side of the anomaly, and thus the wavefront triplicates.
The wavelength of the
wavefield is too short (about 30 m) to observe wavefield
dispersion
and thus the raytracing through the medium slowness
accurately predicts the behavior of the wavefield.
In contrast,
the low-frequency wavefield (Figure
shows the results
of wave-equation modeling with a 60 Hz wavelet
and of raytracing through the
medium slowness.
The rays (dashed lines)
and
the wavefront predicted by raytracing
(solid black line) are
superimposed onto a snapshot of the wavefield.
The wavefield is defocused by the anomaly;
the anomaly causes
a ``shadow zone''
beneath itself,
where the amplitudes are very low.
The high-frequency rays go through a caustic
on either side of the anomaly, and thus the wavefront triplicates.
The wavelength of the
wavefield is too short (about 30 m) to observe wavefield
dispersion
and thus the raytracing through the medium slowness
accurately predicts the behavior of the wavefield.
In contrast,
the low-frequency wavefield (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
behaves quite differently
from the high-frequency one.
The wavefront does not triplicate and although the amplitudes
beneath the anomaly are lower than on the side,
they are not as low as in the high-frequency
wavefield.
The position of the wavefront and the amplitudes of the
wavefield are
well
predicted by raytracing
through the 10 Hz phase slowness computed using the
frequency extrapolation method that I have presented.
Beneath the anomaly,
the distance between the wavefront predicted
by the low-frequency phase slowness
and the one predicted by the medium slowness
is about 20 m; that is, the
conventional eikonal would cause an error of about
)
behaves quite differently
from the high-frequency one.
The wavefront does not triplicate and although the amplitudes
beneath the anomaly are lower than on the side,
they are not as low as in the high-frequency
wavefield.
The position of the wavefront and the amplitudes of the
wavefield are
well
predicted by raytracing
through the 10 Hz phase slowness computed using the
frequency extrapolation method that I have presented.
Beneath the anomaly,
the distance between the wavefront predicted
by the low-frequency phase slowness
and the one predicted by the medium slowness
is about 20 m; that is, the
conventional eikonal would cause an error of about 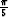 in modeling the propagation of a 10 Hz wavefield through
the anomaly.
in modeling the propagation of a 10 Hz wavefield through
the anomaly.





Next: CONCLUSIONS
Up: Biondi: Solving the frequency-dependent
Previous: Evaluation of derivatives of
Stanford Exploration Project
11/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a vertical slice of the resulting
velocity model for three different frequencies.
The solid line shows the medium slowness; that is, the infinite frequency
slowness. The dashed line shows the phase slowness
at 12.5 Hz, corresponding to a wavelength of 240 m.
Finally the dotted line shows the phase slowness at
5 Hz, corresponding to a wavelength of 600 m.
As frequency decreases,
the frequency extrapolation progressively smooths the slowness
model.
shows a vertical slice of the resulting
velocity model for three different frequencies.
The solid line shows the medium slowness; that is, the infinite frequency
slowness. The dashed line shows the phase slowness
at 12.5 Hz, corresponding to a wavelength of 240 m.
Finally the dotted line shows the phase slowness at
5 Hz, corresponding to a wavelength of 600 m.
As frequency decreases,
the frequency extrapolation progressively smooths the slowness
model.