SEMBLANCE WEIGHTING

All the examples I showed above use linear events just to make the concept clear. In reality there are large amplitude variations across a section. Effects of these large amplitudes can be equalized by using some coherence measure and deriving a weighting function to be applied in the slant stack domain.

Taner et al. (1971) define semblance in general terms. I rewrite their definition in terms of slant stacks:  

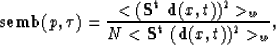$${\rm \bf semb}(p,\tau) = {{ < ({\bf S^t~ d}(x,t))^2 \gt _w }\over{N < {\bf S^t}~ ({\bf d}(x,t))^2 \gt _w}} ,$$ (6)

where N is the number of ``live '' traces used in the slant stack and w is a smoothing window. < ... > denotes simple averaging in that window. The weighting function I applied to the p-$\tau$ domain is a simple step function of the semblance coefficient, killing everything below a certain threshold (let's say 10% of the maximum semblance coefficient). Thus, weak, but spatially coherent events still have a good chance of being recovered, while large but incoherent events are suppressed. The data estimation is now nonlinear (since semb is a nonlinear function of the data) and is described by

 

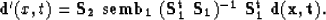$${\bf d'}(x,t) = {\bf S_2}~ {\rm\bf semb_1} ~{\bf (S^t_1~ S_1 )^{-1} }~ {\bf S_1^t}~ {\bf d(x,t)}.$$ (7)

I tried several different weighting functions, such as weighting by powers of energy, but a semblance based weighting was most versatile and effective in my tests.

 

semblance Figure 4 Semblance computed from the stack of the data squared and the squared stack of the data.

 

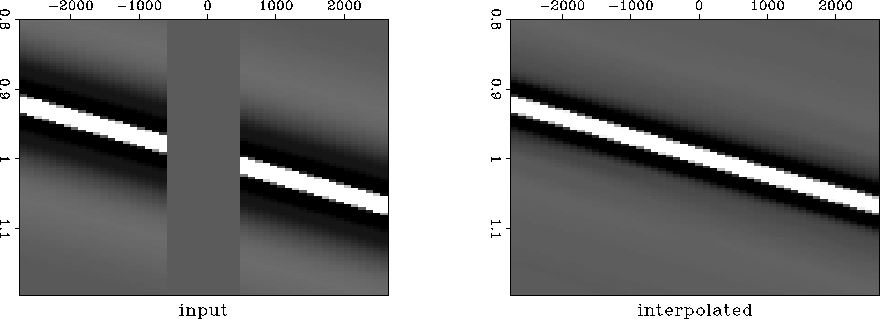
interpolw
Figure 5 Interpolate dead traces and shift using a semblance weighted least squares stack.