Initial conditions

If we assume that the slowness model has a constant value m₀ in the region around source position (x_s,z_s), we can use the following initial conditions for the local paraxial ray method. The traveltimes are

$$\tau(x,z)=s_0\sqrt{(x-x_s)^2+(z-z_s)^2}.$$

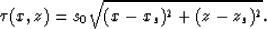
The ray directions are specified by the angles of rays to the vertical, as follows:

$$\theta(x,z)=\arctan{x-x_s \over z-z_s}.$$

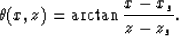
We can also find that

$$M(x,z)={m_0 \over \sqrt{(x-x_s)^2+(z-z_s)^2}}$$

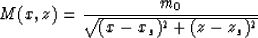
and

$$J(x,z)={1 \over \sqrt{(x-x_s)^2+(z-z_s)^2}}.$$

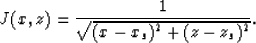
If the slowness varies in this region, the paraxial ray method should be used to find the initial conditions.