




Next: EXAMPLES
Up: Zhang: Interpolation
Previous: CONTINUOUS SIGNALS WITH DISCRETE
The elements in the matrix 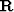 are
are
| 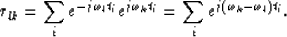 |
(6) |
Because the frequency is uniformly sampled, 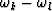 is constant
along diagonals of the matrix; hence the elements of the matrix
is constant
along diagonals of the matrix; hence the elements of the matrix 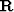 are also constant along its diagonals. Matrices with this kind of structure
are called Toeplitz matrices. Since one can further show
that symmetric elements
with respect to the main diagonal of the matrix are complex conjugates,
the matrix is Hermitian-Toeplitz. Figure
are also constant along its diagonals. Matrices with this kind of structure
are called Toeplitz matrices. Since one can further show
that symmetric elements
with respect to the main diagonal of the matrix are complex conjugates,
the matrix is Hermitian-Toeplitz. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example
of the real and imaginary parts of
shows an example
of the real and imaginary parts of 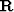 . With a left-side
Hermitian-Toeplitz matrix, equation (5) can be efficiently
solved using the generalized Levinson recursion (Golub and Van Loan, 1989;
Kostov, 1989).
The number of operations required is 2K2, just twice the cost of
multiplying a vector by a matrix.
Once the discrete Fourier spectra are found, equation (2)
can be used to evaluate the continuous signal s(t) at arbitrary positions.
If the evaluations desired are at uniformly spaced positions,
the fast Fourier transform should be used. When the input signal is
uniformly sampled, matrix
. With a left-side
Hermitian-Toeplitz matrix, equation (5) can be efficiently
solved using the generalized Levinson recursion (Golub and Van Loan, 1989;
Kostov, 1989).
The number of operations required is 2K2, just twice the cost of
multiplying a vector by a matrix.
Once the discrete Fourier spectra are found, equation (2)
can be used to evaluate the continuous signal s(t) at arbitrary positions.
If the evaluations desired are at uniformly spaced positions,
the fast Fourier transform should be used. When the input signal is
uniformly sampled, matrix 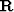 becomes an identity matrix, and the
whole interpolation process is equivalent to the ordinary sinc interpolation.
becomes an identity matrix, and the
whole interpolation process is equivalent to the ordinary sinc interpolation.
The elements of matrix 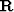 depend only on the
sampling positions, not on the values of samples. Therefore, to interpolate
missing traces, one can pre-compute the inverse of matrix
depend only on the
sampling positions, not on the values of samples. Therefore, to interpolate
missing traces, one can pre-compute the inverse of matrix 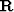 , and then
apply it to each time or frequency slice.
, and then
apply it to each time or frequency slice.
ata
Figure 1 Elements in the matrix  of a general normal equation set:
(a) real part, (b) imaginary part.
of a general normal equation set:
(a) real part, (b) imaginary part.










Next: EXAMPLES
Up: Zhang: Interpolation
Previous: CONTINUOUS SIGNALS WITH DISCRETE
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows an example
of the real and imaginary parts of
shows an example
of the real and imaginary parts of ![]() depend only on the
sampling positions, not on the values of samples. Therefore, to interpolate
missing traces, one can pre-compute the inverse of matrix
depend only on the
sampling positions, not on the values of samples. Therefore, to interpolate
missing traces, one can pre-compute the inverse of matrix ![]() , and then
apply it to each time or frequency slice.
, and then
apply it to each time or frequency slice.
