




Next: CONJUGATE OPERATOR
Up: Ji and Claerbout: Trace
Previous: Ji and Claerbout: Trace
The recursive dip filter, invented by Claerbout (1985),
works in the time and space domain. It is more attractive for seismic data
processing than a dip filter that operates in the frequency-wavenumber domain,
because it can be temporally and spatially nonstationary.
In addition to time and space variability, the recursive dip filter offers
the advantage of a simple and economic recursive implementation.
Let P denote raw data and Q denote filtered data in the frequency-wavenumber
domain. Dip filtering can be achieved by using a low-dip-pass filter:
| 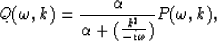 |
(1) |
or a high-dip-pass filter:
| 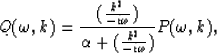 |
(2) |
where 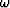 is the temporal frequency, k is the spatial frequency,
and
is the temporal frequency, k is the spatial frequency,
and  determines the cutoff dip (Claerbout, 1985).
determines the cutoff dip (Claerbout, 1985).
To understand the recursive dip filter, we need to examine its amplitude
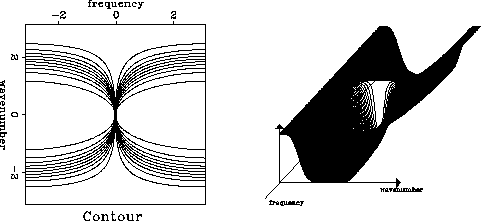
spectrum. Figure 1 shows the amplitude spectrum of a high-dip-pass filter.
The spectrum changes slowly from a pass zone to a reject zone.
This is the only drawback of recursive filters, however, the transition zone
need not be short in our application to trace interpolation.
fig1
Figure 1 Left: contour plot
of the amplitude spectrum of a high-pass recursive dip filter with
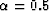 Right: 3D plot of the amplitude spectrum of the same filter.
Right: 3D plot of the amplitude spectrum of the same filter.





The realization of equations (1) and (2) is obtained by replacing
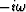 and -k2 with
and -k2 with 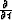 and
and
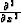 , respectively.
Clearing out all the fractions in equation (1) then leads t the following
partial-differential equation:
, respectively.
Clearing out all the fractions in equation (1) then leads t the following
partial-differential equation:
| 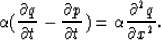 |
(3) |
Approximating the derivative by a difference operator gives the desired
recursive relations (Claerbout, 1985).
For example, the low-pass filter becomes
| 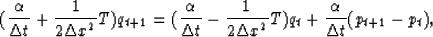 |
(4) |
where T represents a tridiagonal matrix with ( 1, -2, 1 ) along the diagonal,
and  determines the cutoff dip.
For a stable and accurate implementation,
we apply the Crank-Nicholson method and the 1/6 trick.
The result is the following differencing star:
determines the cutoff dip.
For a stable and accurate implementation,
we apply the Crank-Nicholson method and the 1/6 trick.
The result is the following differencing star:
where 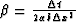 and
and 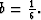
Implementation of the above differencing star is straightforward.
However, in order to develop the forward and transpose operators needed
for iterative application, we need to write these operators in a matrix
form as shown in the following section.





Next: CONJUGATE OPERATOR
Up: Ji and Claerbout: Trace
Previous: Ji and Claerbout: Trace
Stanford Exploration Project
12/18/1997
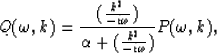
![]() and -k2 with
and -k2 with ![]() and
and
![]() , respectively.
Clearing out all the fractions in equation (1) then leads t the following
partial-differential equation:
, respectively.
Clearing out all the fractions in equation (1) then leads t the following
partial-differential equation: