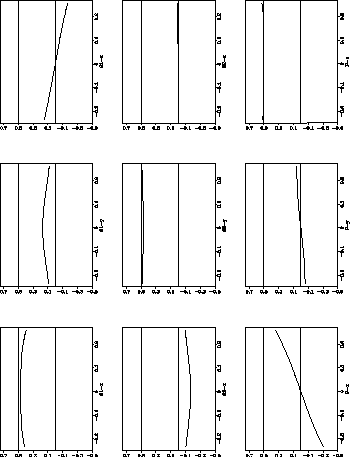
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a plot
of the amplitude of one element of the
is a plot
of the amplitude of one element of the
To examine the validity of the approximation I numerically calculated
the exact operators for an orthorhombic medium. The elastic constants
for this medium were generated by calculating the elastic constants
for a layered medium with plane-vertical cracks at ![]() to the
x-axis. Each graph in the grid of figure
to the
x-axis. Each graph in the grid of figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is a plot
of the amplitude of one element of the
is a plot
of the amplitude of one element of the ![]() separation operator
as a function of slowness. If the first order approximation is
exactly valid the symmetric elements would be horizontal lines and the
anti-symmetric elements would be lines with constant slope. Clearly,
the first order approximation is not exact. However it is a
reasonable approximation for a range of slownesses around zero.
separation operator
as a function of slowness. If the first order approximation is
exactly valid the symmetric elements would be horizontal lines and the
anti-symmetric elements would be lines with constant slope. Clearly,
the first order approximation is not exact. However it is a
reasonable approximation for a range of slownesses around zero.
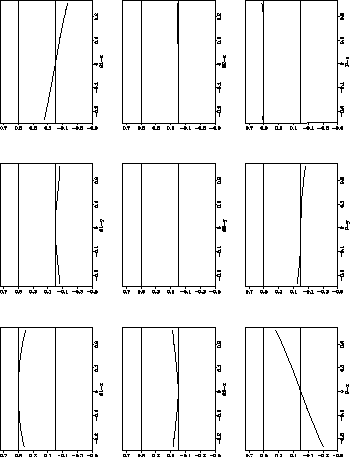
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the exact operator after a coordinate
frame rotation of
shows the exact operator after a coordinate
frame rotation of ![]() has been applied. This operator should
be the combination of the second and third stages of the separation
process. Note that the scaling by 0.5 has not been accounted for in
this transformation. If the first order approximation and the
separation of the rotation operator were exact we would expect to see
a flat line at 0.5 for each of the symmetric elements and a straight
line passing through (0.,0.) for the anti-symmetric elements. Again
the first order approximation is good for a reasonable range of
slownesses. The slownesses are expressed in sec./km. The first order
approximation appears to be reasonable for slowness values up to 0.15,
which for this medium corresponds to a P-wave propagating at 45 degrees
to the vertical and an S-wave propagating at 25 degrees to the
vertical. This are both large angles for typical surface
seismic experiments. I consider the first order approximation to be a
reasonable one for this set of elastic constants. Whether it is always a good
approximation is a topic that needs further study.
has been applied. This operator should
be the combination of the second and third stages of the separation
process. Note that the scaling by 0.5 has not been accounted for in
this transformation. If the first order approximation and the
separation of the rotation operator were exact we would expect to see
a flat line at 0.5 for each of the symmetric elements and a straight
line passing through (0.,0.) for the anti-symmetric elements. Again
the first order approximation is good for a reasonable range of
slownesses. The slownesses are expressed in sec./km. The first order
approximation appears to be reasonable for slowness values up to 0.15,
which for this medium corresponds to a P-wave propagating at 45 degrees
to the vertical and an S-wave propagating at 25 degrees to the
vertical. This are both large angles for typical surface
seismic experiments. I consider the first order approximation to be a
reasonable one for this set of elastic constants. Whether it is always a good
approximation is a topic that needs further study.
 |
 |