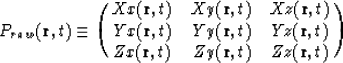
In a nine-component seismic, survey sources and receivers are oriented along each of the three coordinate axes. The experiment is recorded for every combination of source and receiver orientation. The recorded wavefield may be represented as a matrix of data; the rows correspond to the direction of the source and the columns to the direction of the receiver. Each element of the matrix is one shot record.
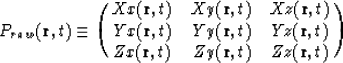
The nine-components that we wish to process are those that correspond to downgoing waves of one wavetype at the source and upcoming waves of one wavetype at the receiver. We can represent this data as a new matrix where the rows correspond to the downgoing wavetype at the source and the columns correspond to the upcoming wavetype at the receiver.
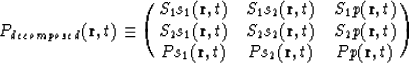
![]()
As many authors have noted, this transformation is best performed in
the ![]() domain or the
domain or the ![]() domain as the
operators are functions of the horizontal slowness. I choose to
perform the decomposition in the
domain as the
operators are functions of the horizontal slowness. I choose to
perform the decomposition in the ![]() domain so that I can
use a trace-by-trace method rather than a sample-by-sample method.
domain so that I can
use a trace-by-trace method rather than a sample-by-sample method.