




Next: Nonlinear scheme
Up: WEIGHTED LEAST-SQUARES
Previous: WEIGHTED LEAST-SQUARES
As indicated in the examples, the basic scheme of equation (4)
suppress part of the multiples but also interferes with the nearby primaries.
Furthermore, the converted waves are suppressed in conjunction with
the multiples. The deterioration of the primaries is caused by the fact
that some of energy associated with the primaries extends over the windowed
region and the operator, as defined in equation (4), acts
uniformly over all the window. A possible solution for that is to use a
weighting function, designed to privilege the more energetic
regions inside the window, which are more likely related to multiples.
Equation (4) is replaced in this case by
| 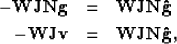 |
(4) |
| |
where 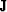 is a diagonal weighting operator chosen to represent
an approximation for the noise (multiples) covariance matrix. We have chosen
the operator
is a diagonal weighting operator chosen to represent
an approximation for the noise (multiples) covariance matrix. We have chosen
the operator 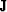 to be the smoothed semblance velocity spectrum of the
original data (Figure
to be the smoothed semblance velocity spectrum of the
original data (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -a).
-a).





Next: Nonlinear scheme
Up: WEIGHTED LEAST-SQUARES
Previous: WEIGHTED LEAST-SQUARES
Stanford Exploration Project
12/18/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -a).
-a).