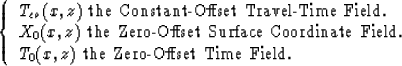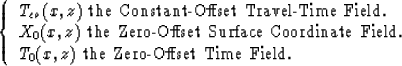The two conjugate MZO operators

Spreading data along the MZO impulse response is identical to summing along a conjugate curve. For zero-offset migration in a constant velocity medium, this is equivalent to saying: spreading the data over circles produces a result identical to summing along hyperbolas. From a computational point of view, the spreading operator (ellipse for DMO, circle for constant velocity migration) is a ``PUT'' operator, meaning that the operator takes a time sample and puts it in all the adjacent traces. The conjugate summation operator (hyperbola for constant velocity migration) is a ``GET'' operator because it gets the input from the adjacent traces.

By using finite-difference travel-time maps, both the ``GET'' and ``PUT'' operators can be calculated in very similar ways:

1.

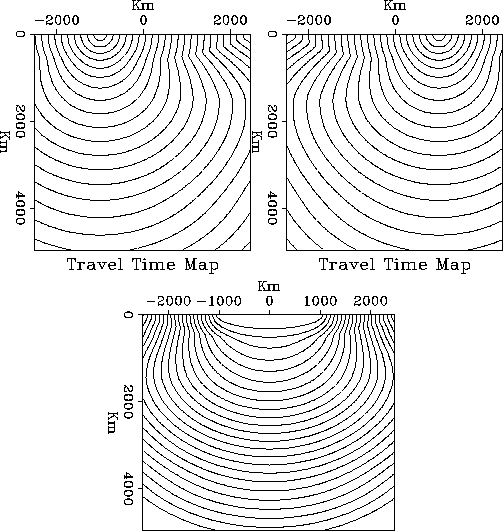
Compute a travel-time map for the source given a velocity model v(x,z). Figure 1a is an example of a travel-time field calculated with the source located at X=-1000.

2.

Compute a travel-time map with the source in the receiver location, given the same velocity model. Figure 1b is an example of a travel-time field calculated with the receiver located at X=1000.

3.

Sum the two travel-time maps. In each location of the grid we have the sum of the travel-time from source to receiver T_co(x,z). Figure 1c is an example of a constant-offset travel-time field calculated by summing the source and receiver travel-time fields.

4.

The gradient of the constant-offset travel-time field T_co(x,z) is a vector which has the same direction as the zero-offset ray. In other words, the vector perpendicular to a constant-offset isochron bisects the angle between the ray coming from the source and the one returning to the receiver. This is obvious for some people, however, I demonstrate this proposition in the Appendix. Therefore, by calculating the gradient of the constant-offset travel-time map in each point of the grid, we can find the ray direction for the zero-offset case for each grid point.

5.

Using the gradient table we can compute for each grid location the surface coordinate of the zero-offset X₀(x,z), which is equivalent to finding the intersection of the surface with the zero-offset ray.

6.

Using the gradient table we can compute for each grid location the zero-offset travel-time T₀(x,z) along each zero-offset ray.

The algorithm is identical up to this point for the two conjugate operators. At this time there are three tables for our grid velocity model:

$$\left \{ \begin{array} {l} T_{co}(x,z) \mbox{ the Constant-O... ..._0(x,z) \mbox{ the Zero-Offset Time Field. }\end{array} \right.$$

 

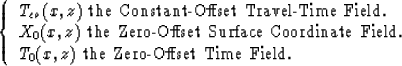
Rayabc
Figure 1 (a) Travel-time from a source located at X=-1000. (b) Travel-time from a source located at X=1000. (c) Isochrons for a constant-offset model (h=1000).

The PUT operator is obtained by associating for each value of T_co(x,z) a pair of coordinates (T₀(x,z),X₀(x,z)). In other words, for a given value of the Constant-Offset Travel-Time, we find an isochron T_co(x,z)=t_h=constant of coordinates (x,z) and the values of the X₀(x,z) and T₀(x,z) associated with that curve. The resulting operator is a function of X₀(x,z) and T₀(x,z) and a parameter t_h=T_co(x,z)=constant. Therefore, we can write it in the form P(T₀(x,z),X₀(x,z);t_h) where the parameter t_h fixes the curve T_co(x,z)=constant.

The GET operator can be defined in a similar way by associating for each value of T₀(x,z) a pair of coordinates (T_co(x,z),X₀(x,z)). In other words, for a given value of the Zero-Offset Time Field, we find an isochron T₀(x,z)=t₀=constant of coordinates (x,z) and the values of the X₀(x,z) and T_co(x,z) associated with that curve. The resulting operator is a function of X₀(x,z) and T_co(x,z) and a parameter t₀=T₀(x,z)=constant. Therefore, we can write it in the form G(T_co(x,z),X₀(x,z);t₀) where the parameter t₀ fixes the curve T₀(x,z)=constant. From the above formulation one can see the two operators (PUT and GET) are conjugate (adjoint) operators.

In practice, I obtain the PUT operator using a binary search algorithm in the table T_co(x,z) ( the binary search is possible because the velocity model is depth variable v(z)) and I store all pairs of values (T₀(x,z),X₀(x,z)) corresponding to an input time sample, which allows for all possible triplications in the operator. For a laterally varying velocity the binary search can be replaced with a linear search. The GET operator is obtained using a binary search algorithm in the table T₀(x,z) and by storing all the pairs of values (T_co(x,z),X₀(x,z)) corresponding to an output time sample.

 

model16
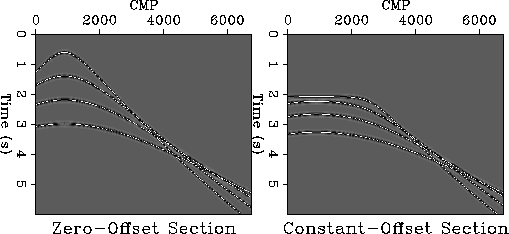
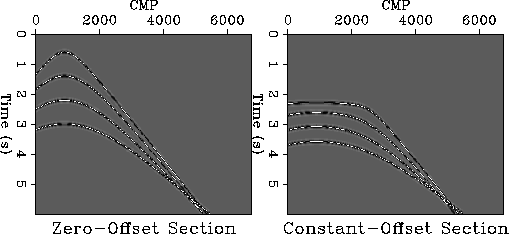
Figure 2 Zero-offset section and maximum constant-offset section for the constant gradient velocity.

 

model46
Figure 3 Zero-offset section and maximum constant-offset section for the depth variable velocity.

 

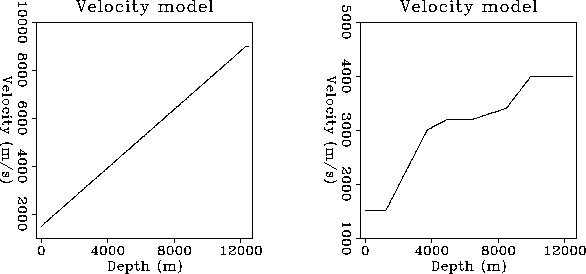
Velm1m4
Figure 4 Velocity models for the two cases considered.