




Next: 12: OPERATOR OF INTEGRAL
Up: 11: TRUE AMPLITUDE MIGRATION
Previous: CSP migration, 3D case
There is a remarkable relationship between the amplitude 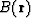 of a
discontinuity
on zero-offset migrated sections and the amplitude
of a
discontinuity
on zero-offset migrated sections and the amplitude 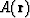 of the corresponding
discontinuity on a CSP section for the point R that belongs to the
same normal ray:
of the corresponding
discontinuity on a CSP section for the point R that belongs to the
same normal ray:
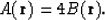
This means that we can use the formulas for CSP patterns at s=r; the
constant factor of 4 doesn't play any role. If we take into account the
equality
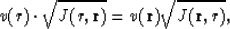
we receive
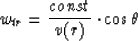
and
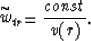
The operator 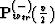 is not unique. If the
medium is homogeneous then there is a whole family of operators
is not unique. If the
medium is homogeneous then there is a whole family of operators
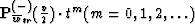 that acts according to the formula:
that acts according to the formula:
![\begin{displaymath}
U^{(-)} = {\bf P}_{{\overline{w}}_{m}}^{(-)} ({v \over 2}) [ t^m U_0],\end{displaymath}](img660.gif)
and
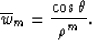
In the 2D case the amplitude of the image depends on the radius of
transverse curvature of the reflector. But if the reflector is planar
or cylindrical, we have a family of true-amplitude operators of the
same type as
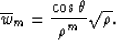





Next: 12: OPERATOR OF INTEGRAL
Up: 11: TRUE AMPLITUDE MIGRATION
Previous: CSP migration, 3D case
Stanford Exploration Project
1/13/1998
![]()
![]()
![]()
![]()
![]() is not unique. If the
medium is homogeneous then there is a whole family of operators
is not unique. If the
medium is homogeneous then there is a whole family of operators
![]() that acts according to the formula:
that acts according to the formula:
![]()
![]()
![]()