|
|
|
|
Aligning microseismic reflections for imaging |
|
|---|
|
useisfigurestew
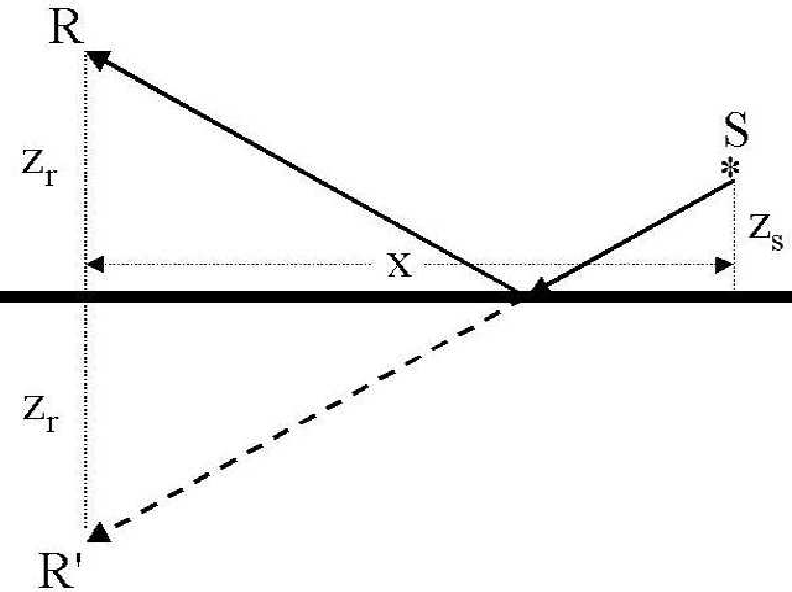
Figure 5. Diagram showing source-receiver relative locations with respect to the reflector. |
|
|
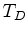 , is given by
, is given by
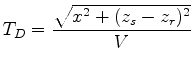
and the reflected arrival time,
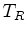 , is similarly
, is similarly
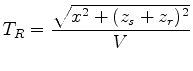 .
.
To calculate the relative effect of small shifts in source or receiver location
on these arrival times,
we compute the gradients
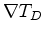 and
and
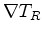 with respect to changes in source location:
with respect to changes in source location:
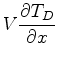 |
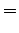 |
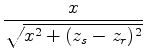 |
|
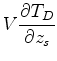 |
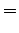 |
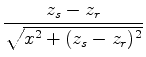 |
|
 |
|||
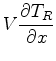 |
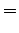 |
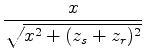 |
|
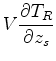 |
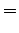 |
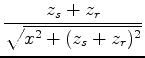 |
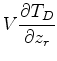 |
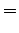 |
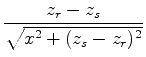 |
|
 |
|||
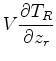 |
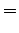 |
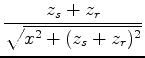 |
With these gradients in hand, let 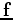 be a unit vector aligned with the fracture and
be a unit vector aligned with the fracture and 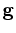 be a unit vector
aligned with the receiver array. Then the directional derivatives
be a unit vector
aligned with the receiver array. Then the directional derivatives
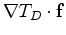 and
and
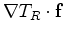 give the relative sensitivities of the direct and reflected arrival times to source
displacement along the fault that gave rise to some set of multiplets. Similarly, the directional derivatives
give the relative sensitivities of the direct and reflected arrival times to source
displacement along the fault that gave rise to some set of multiplets. Similarly, the directional derivatives
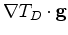 and
and
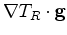 provide the arrival slopes of the direct and reflected
arrivals respectively.
provide the arrival slopes of the direct and reflected
arrivals respectively.
With the above, not only can we estimate where to look for weak reflections behind
a direct arrival (or, conversely,
how far from the microseismic source a clear reflection arose), but
we can also begin to understand how much or little reflections within multiplets
misalign when their associated direct arrivals are aligned. For example, the limiting
case of the receiver just above the reflector has the reflected and direct arrivals
arriving at the same time and changing at the same rate as the source is displaced whereas
if
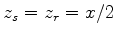 the reflected arrival displaces
the reflected arrival displaces 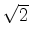 times further than the
direct arrival. Both of these cases are serendipitous in the sense that aligning the
direct arrival across channels also aligns the reflected arrival.
times further than the
direct arrival. Both of these cases are serendipitous in the sense that aligning the
direct arrival across channels also aligns the reflected arrival.
Let us apply these formulas to analyze the shear reflection we spotted in our Bonner multiplet example.
In the example of Figure 1, the receivers are at about 12,800 ft depth and the microseismic source was computed to be at about 13,100 ft depth and an offset of about 300 ft from the monitor well. The dipole sonic log shows a compressional velocity of about 13,750 ft/sec and a shear velocity of about 8,000 ft per second in that depth range. The difference between the direct P and the direct S arrivals would be 22 msec, in good agreement with the actual record. The delay of about 220 msec to the later shear arrival corresponds to a reflector depth of about 13,800, i.e., a thousand feet below the receivers and, sigh, well below the reservoir depth.
|
|
|
|
Aligning microseismic reflections for imaging |