Estimation of Q from surface-seismic reflection data in data space and image space

Estimation of Q from data space

Because this simple 2D example has no complex structure or noise, I apply a data-space QVO method to this model before going to the image domain. According to the theory developed by Quan and Harris (1997), the central-frequency shift changes with attenuation in the way described in equation 7. If the wave travels in the homogeneous media and reflected from one flat reflector, equation 7 can be simplified in the following way,

$$x^2 + z^2 = C^2 \Delta f^2 Q^2,$$ (10)

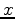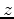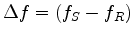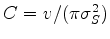where $x$ is offset, $z$ is depth, $\Delta f =(f_S - f_R )$ , and $C = v/(\pi \sigma _S^2 )$ , which is a constant if I assume the velocity and the variance of the source are known.

trec50,trec99999,fpeak50,fpeak99999
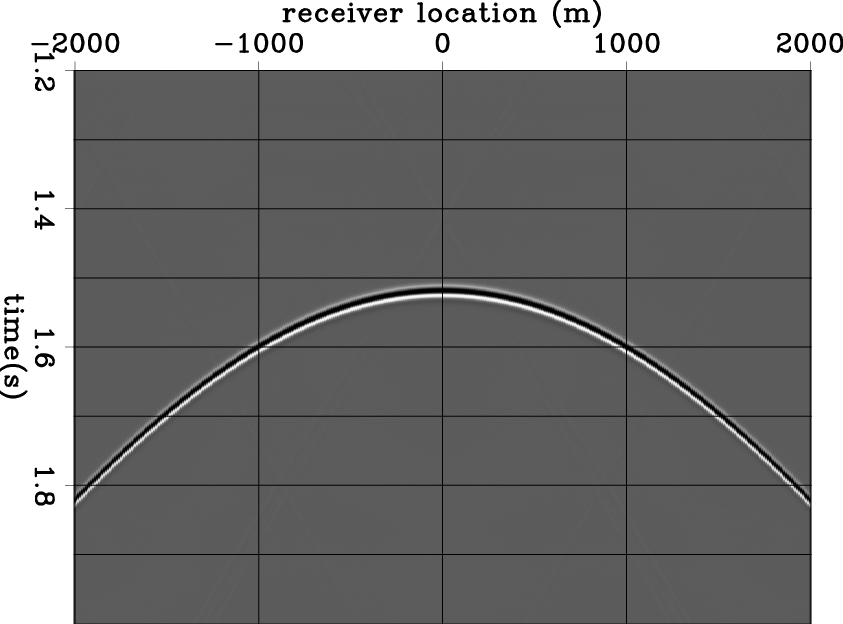
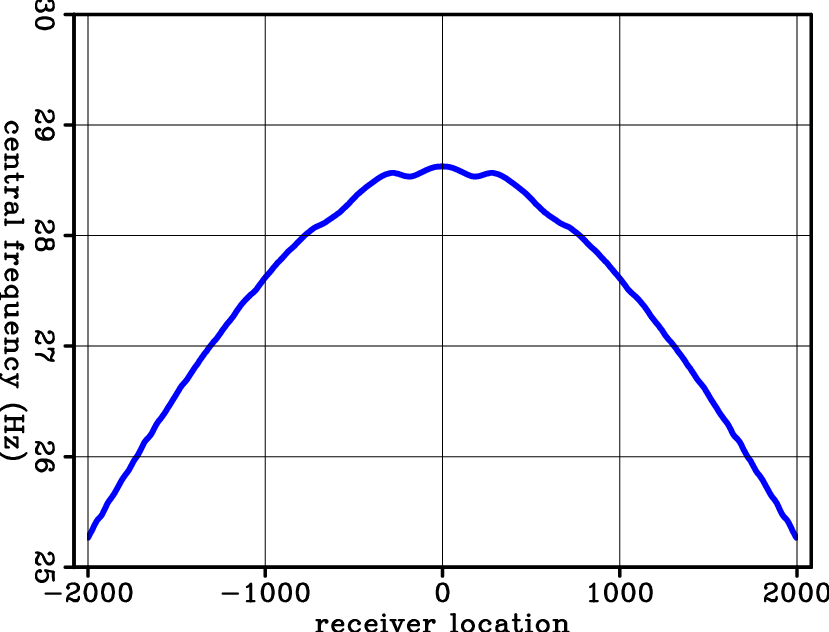
Figure 1. Given the 2D synthetic example, (a) modeled data with attenuation (Q=50); (b) modeled data without attenuation (Q=99999); (c) central frequency with attenuation; (d) central frequency without attenuation.

Equation 10 relates four variables: two coordinates of the data space 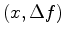$(x,\Delta f)$ and two of the model space 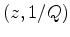$(z, 1/Q)$ . An impulse in model space corresponds to a hyperbola in data space. In the opposite case, an impulse at a point in data space corresponds to another hyperbola in the model space. If I sum along the trajectories in the data space, energy will be concentrated in the model space to indicate the Q value. In this paper, I define the model space as the Q-spectra and the procedure described above as the Q-scan. Least-squares inversion can also be used here to yield a better result.

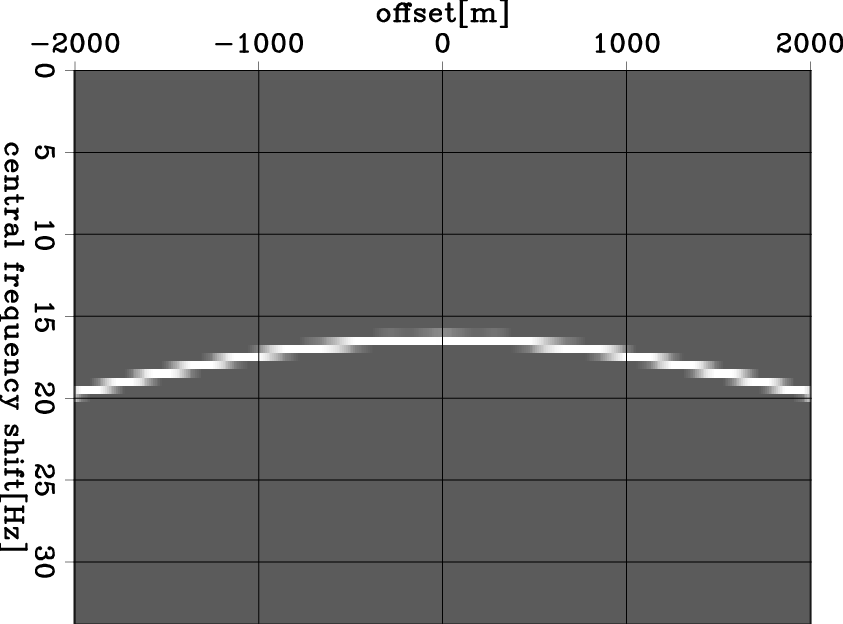
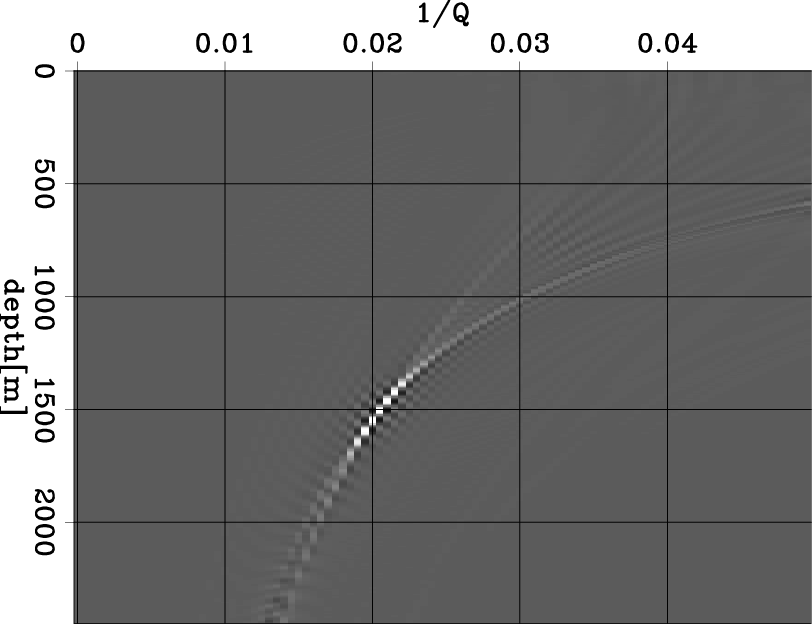
Figure 2(a) shows the central-frequency shift of the modeled data in Figure 1(a). After scanning, I compute the Q-spectra in Figure 2(b). This result shows concentrated energy around the expected point (1500 m, 0.02), which indicates that the RMS Q is 50 above 1500 m depth. Figure 2(c) shows least-squares inversion after 50 iterations. The energy is more focused on the expected point and shows much higher resolution. Therefore, I conclude that computing the Q-spectra can be used in estimating the RMS Q for a model with simple structure.

df,Qscanadj,Qscaninv
Figure 2. Figure 2(a) shows the central-frequency shift of the modeled data in Figure 1(a). The Q-spectra is computed in Figure 2(b). This result shows concentrated energy around the expected point (1500 m, 0.02), which indicates that the RMS Q is 50 above 1500 m depth. Figure 2(c) shows least-squares inversion after 50 iterations. The energy is more focused on the expected point and shows much higher resolution.

In reality, however, this data-domain method can be inaccurate when lateral velocity variations and dipping structures exist. Therefore, image-domain methods is needed to more accurately estimate Q.

Estimation of Q from surface-seismic reflection data in data space and image space