|
|
|
|
Polarity preserving decon in ``N log N'' time |
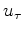 we may make improvements
on the old mathematical method
of blind deconvolution.
We were uncommonly successful here
in dealing with our most commonly observed wavelet, the Ricker wavelet.
This success suggests other improvements
might flow from manipulations of the
we may make improvements
on the old mathematical method
of blind deconvolution.
We were uncommonly successful here
in dealing with our most commonly observed wavelet, the Ricker wavelet.
This success suggests other improvements
might flow from manipulations of the 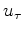 for other purposes.
for other purposes.
For example, given only a single seismogram,
we may wish to limit the number of degrees of freedom for the filter estimation.
We have long known this can be done by smoothing the data spectrum.
Another method is to limit the range, or taper the range of 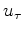 coefficients.
Such ideas are untried, so not yet compared.
coefficients.
Such ideas are untried, so not yet compared.
Likewise, many shot waveforms have been recorded and tabulated.
Perhaps it makes sense to map these wavelets to the ``lag-log'' space 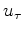 to better understand their statistics.
to better understand their statistics.
I see no immediate application, but we might recall that spectral factorization is also applicable for complex-valued signals. Then the spectrum is non-symmetric. This arises when time-dependent signals have been previously Fourier transformed over space.
Shuki asks, ``What about seafloor receivers where there is one ghost, not two?''
I reply, ``Perhaps the same code can be used, but instead of gateing on
the range 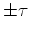 being 3/4 period for the Ricker wavelet,
it might be instead 1/4 period for the the primary lobe.
being 3/4 period for the Ricker wavelet,
it might be instead 1/4 period for the the primary lobe.
|
|
|
|
Polarity preserving decon in ``N log N'' time |