 |
 |
 |
 | Fast automatic wave-equation migration velocity analysis using encoded simultaneous sources |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Tang: Encoded simultaneous-source WEMVA
Previous: conclusions
-
Albertin, U., P. Sava, J. Etgen, and M. Maharramov, 2006, Adjoint
wave-equation velocity analysis: SEG Technical Program Expanded Abstracts,
25, 3345-3349.
-
-
Beasley, C. J., 2008, A new look at marine simultaneous sources: The Leading
Edge, 27, 914-917.
-
-
Beasley, C. J., R. E. Chambers, and Z. Jiang, 1998, A new look at simultaneous
sources: SEG Technical Program Expanded Abstracts, 17, 133-135.
-
-
Ben-Hadj-Ali, H., S. Operto, and J. Virieux, 2011, An efficient
frequency-domain full waveform inversion method using simultaneous encoded
sources: Geophysics, 76, R109-R124.
-
-
Berkhout, A. J. G., 2008, Changing the mindset in seismic data acquisition:
The Leading Edge, 27, 924-938.
-
-
Biondi, B. and P. Sava, 1999, Wave-equation migration velocity analysis: SEG
Technical Program Expanded Abstracts, 18, 1723-1726.
-
-
Dai, W., C. Boonyasiriwat, and G. T. Schuster, 2010, 3D multi-source
least-squares reverse time migration: SEG Technical Program Expanded
Abstracts, 29, 3120-3124.
-
-
Dai, W. and J. Schuster, 2009, Least-squares migration of simultaneous sources
data with a deblurring filter: SEG Technical Program Expanded Abstracts, 28, 2990-2994.
-
-
Fei, W., P. Williamson, and A. Khoury, 2009, 3-D common-azimuth
wave-equation migration velocity analysis: SEG Technical Program Expanded
Abstracts, 28, 2283-2287.
-
-
Hampson, G., J. Stefani, and F. Herkenhoff, 2008, Acquisition using
simultaneous sources: The Leading Edge, 27, 918-923.
-
-
Krebs, J. R., J. E. Anderson, D. Hinkley, R. Neelamani, S. Lee, A. Baumstein,
and M.-D. Lacasse, 2009, Fast full-wavefield seismic inversion using encoded
sources: Geophysics, 74, WCC177-WCC188.
-
-
Liu, F., D. W. Hanson, N. D. Whitmore, R. S. Day, and R. H. Stolt, 2006,
Toward a unified analysis for source plane-wave migration: Geophysics, 71, no. 4, S129-S139.
-
-
Romero, L. A., D. C. Ghiglia, C. C. Ober, and S. A. Morton, 2000, Phase
encoding of shot records in prestack migration: Geophysics, 65,
426-436.
-
-
Sava, P. and I. Vlad, 2008, Numeric implementation of wave-equation migration
velocity analysis operators: Geophysics, 73, VE145-VE159.
-
-
Shen, P., 2004, Wave-equation migration velocity analysis by differential
semblance optimization: PhD thesis, Rice University.
-
-
Shen, P., W. W. Symes, S. Morton, A. Hess, and H. Calandra, 2005, Differential
semblance velocity analysis via shot profile migration: SEG Technical Program
Expanded Abstracts, 24, 2249-2252.
-
-
Soubaras, R. and B. Gratacos, 2007, Velocity model building by semblance
maximization of modulated-shot gathers: Geophysics, 72, U67-U73.
-
-
Stolt, R. H. and A. Benson, 1986, Seismic migration: Theory and practice:
Geophysical Press.
-
-
Tang, Y., 2011, Imaging and velocity analysis by target-oriented wavefield
inversion: PhD thesis, Stanford University.
-
-
Tang, Y. and B. Biondi, 2009, Least-squares migration/inversion of blended
data: SEG Technical Program Expanded Abstracts, 28, 2859-2863.
-
-
Tang, Y., C. Guerra, and B. Biondi, 2008, Image-space wave-equation tomography
in the generalized source domain: SEP-136, 1-22.
-
-
Tang, Y. and S. Lee, 2010, Preconditioning full waveform inversion with
phase-encoded Hessian: SEG Technical Program Expanded Abstracts, 29,
1034-1038.
-
-
Whitmore, N. D., 1995, An imaging hierarchy for common angle plane wave
seismogram: PhD thesis, University of Tulsa.
-
-
Zhang, Y., J. Sun, C. Notfors, S. H. Gray, L. Chernis, and J. Young, 2005,
Delayed-shot 3D depth migration: Geophysics, 70, E21-E28.
-
Appendix
A
Equivalence of image-stack-power maximization and data-domain Born wavefield inversion
This appendix shows that maximizing the image stack power (or minimizing its negative) is equivalent to Born wavefield inversion, which
minimizes the difference between the modeled and observed primaries.
The difference-based objective function for data-domain Born wavefield inversion can be defined as follows:
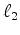 |
|
|
(19) |
where
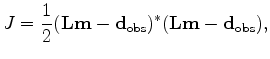 is the observed data vector,
is the observed data vector,
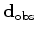 is the reflectivity vector;
is the reflectivity vector;
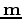 is the Born modeling operator that only modeled the angle stacked reflectivity (zero-subsurface-offset reflectivity),
which is a function of the velocity vector
is the Born modeling operator that only modeled the angle stacked reflectivity (zero-subsurface-offset reflectivity),
which is a function of the velocity vector 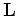 . Objective function A-1 is minimized by
optimizing both
. Objective function A-1 is minimized by
optimizing both 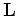 and
and 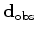 .
Expanding equation A-1 yields
.
Expanding equation A-1 yields
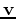 |
|
|
(20) |
In the least-squares sense, the reflectivity model 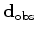 can be formally obtained as follows, assuming the Hessian
can be formally obtained as follows, assuming the Hessian 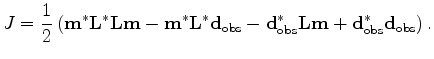 is invertible:
is invertible:
 |
|
|
(21) |
Substituting equations A-3 into A-2 and simplifying yield
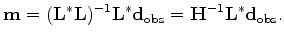 |
|
|
(22) |
Since
 is a constant, it can be ignored in the above equation, therefore
is a constant, it can be ignored in the above equation, therefore
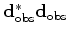 |
|
|
(23) |
Note that the migration image
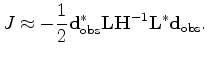 is defined as follows:
is defined as follows:
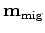 |
|
|
(24) |
Substituting equations A-6 into A-5 yields
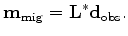 |
|
|
(25) |
To simplify the problem, I ignore the Hessian 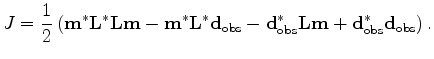 in equation A-7 and assume
it to be an identity matrix. Therefore, equation A-7 becomes
in equation A-7 and assume
it to be an identity matrix. Therefore, equation A-7 becomes
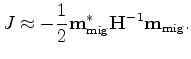 |
|
|
(26) |
which is the same as equation 1 defined in the body of the paper.
However, the Hessian 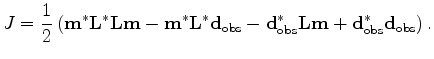 in equation A-7 might be important,
especially in complex geologies, where the illumination is distorted by complex overburdens.
The importance of the Hessian in equation A-7 remains an area for further investigation.
in equation A-7 might be important,
especially in complex geologies, where the illumination is distorted by complex overburdens.
The importance of the Hessian in equation A-7 remains an area for further investigation.
 |
 |
 |
 | Fast automatic wave-equation migration velocity analysis using encoded simultaneous sources |  |
![[pdf]](icons/pdf.png) |
Next: About this document ...
Up: Tang: Encoded simultaneous-source WEMVA
Previous: conclusions
2011-09-13
 is the observed data vector,
is the observed data vector,
![]() can be formally obtained as follows, assuming the Hessian
can be formally obtained as follows, assuming the Hessian 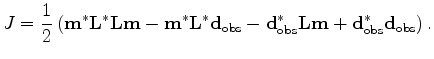 is invertible:
is invertible:
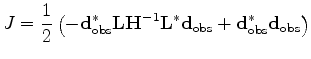 is a constant, it can be ignored in the above equation, therefore
is a constant, it can be ignored in the above equation, therefore
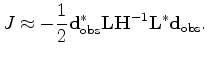 is defined as follows:
is defined as follows:
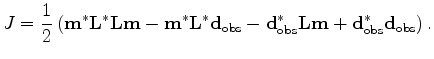 in equation A-7 and assume
it to be an identity matrix. Therefore, equation A-7 becomes
in equation A-7 and assume
it to be an identity matrix. Therefore, equation A-7 becomes
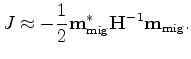
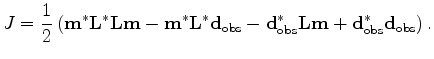 in equation A-7 might be important,
especially in complex geologies, where the illumination is distorted by complex overburdens.
The importance of the Hessian in equation A-7 remains an area for further investigation.
in equation A-7 might be important,
especially in complex geologies, where the illumination is distorted by complex overburdens.
The importance of the Hessian in equation A-7 remains an area for further investigation.
![\fbox{\includegraphics[width=14cm]{/net/server/wrk/sep145/Filler/Fig/yaxun-filler.pdf}}](img90.png)