Data examples of logarithm Fourier-domain bidirectional deconvolution

METHODOLOGY

Claerbout et al. (2011) show the complete derivation of the method. Here, we describe only the major steps of this method. As with any iterative method, we have two issues to solve in one iteration: the update direction and the step length of the update. Below, we disscuss how we can solve these two issues in the logarithm Fourier-domain method.

As we discussed in the previous section, we can decompose the arbitrary data 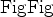$d$ into three parts: the reflectivity series $r$ , the minimum phase wavelet $w_a$ and the maximum phase wavelet $w_b$ :

$$d = r*(w_a *w_b).$$ (1)

We wish to solve for the deconvolution filters $a$ and $b$ , which should be the inverses of wavelets $w_a$ and $w_b$ :

$$\left\{ \begin{array}{l} w_a*a = \delta (n) \\ w_b*b = \delta (n) \end{array} . \right.$$ (2)

From equation 2, we know that $a$ is minimum phase and $b$ is maximum phase. If we know the deconvolution filters $a$ and $b$ , we can get reflectivity series $r$ as follows:

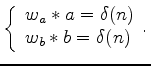$$r = d*a *b .$$ (3)

Next we transform our problem into the Fourier domain. We use capital letters to denote variables in the Fourier domain:

$$R=DAB.$$ (4)

We use $U$ to denote the logarithm of the product of $A$ and $B$ :

$$U={\rm log}(AB).$$ (5)

Our problem then becomes

$$R=De^U,$$ (6)

where $U$ has become our new unknown in bidirectional deconvolution, and we want to update it in each iteration. After some derivation (Claerbout et al., 2011), we get, in the time domain,

$$\left\{ \begin{array}{l} \Delta u = r^\circledast{\rm Hyp}'(r) \\ \Delta r = r*\Delta u \end{array} , \right.$$ (7)

where $^\circledast$ means cross-correlation and ${\rm Hyp}(r_i)=\sqrt{r_i^2+R_0^2}-R_0$ is the hyperbolic penalty function.

By Newton's method (using the only first 2 terms of the Taylor expansion), we can calculate the step length $\alpha$ :

$$\alpha=\frac{\sum_i{\rm Hyp}'(r_i)\Delta r_i}{\sum_i{\rm Hyp}''(r_i)\Delta r_i^2} .$$ (8)

Because we use Newton's method, this step length $\alpha$ calculated above is not the final value. To obtain the final step length at each iteration, we need another iteration (nested or second-order iteration):

Given the update directions (both for the unknown $u$ and for the residual $r$ ) and the step length $\alpha$ of the update, we have everything we need for each iteration. We can iterate to convergence.

Data examples of logarithm Fourier-domain bidirectional deconvolution