Predicting rugged water-bottom multiples through wavefield extrapolation with rejection and injection

Wavefield extrapolation with rejection and injection

The idea of this method comes from the fact that water-bottom multiples and peg-legs are trapped between the water bottom and sea surface, as shown in figure 1. Therefore, when we input the shot gather on the sea surface and perform downward wavefield extrapolation, the down-going wave below the water-bottom can be rejected. Similarly, when we inject the recorded down-going wavefield at the water bottom and perform the upward wavefield extrapolation, the up-going wave below the water bottom also can be rejected.

Obviously, based on the above-mentioned idea, an auxiliary model presentation should be given. As shown in figure 2, in this auxiliary model presentation, the solid circle, rectangle and star represent the nodes of computation in water, in the subsurface, and on the water bottom, respectively.

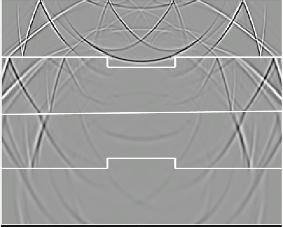
fig1
Figure 1. A snapshot of seismic modeling to show the water bottom multiples and illustrate wavefield rejection and injection. [NR]

fig2
Figure 2. The auxiliary model presentation for wavefield extrapolation with wavefield rejection and injection. [NR]

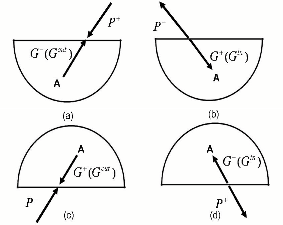
fig3
Figure 3. Schematic illustration of the four types of wavefield extrapolations in terms of Kirchhoff integral: (a) downward wavefield extrapolation of the down-going wave; (b) downward wavefield extrapolation of the up-going wave; (c) upward wavefield extrapolation of the up-going wave; and (d) upward wavefield extrapolation of the down-going wave. [NR]

Predicting rugged water-bottom multiples through wavefield extrapolation with rejection and injection