 |
 |
 |
 | A new method for more efficient seismic image segmentation |  |
![[pdf]](icons/pdf.png) |
Next: Approach
Up: Halpert: Faster image segmentation
Previous: Introduction
As mentioned previously, graph-based segmentation methods are popular for automating salt interpretation. More specifically, the eigenvector-based Normalized Cuts Image Segmentation (NCIS) algorithm (Shi and Malik, 2000) has attracted a great deal of interest because of its capability to capture global aspects of the image, rather than just track local features. Local feature trackers are ubiquitous in seismic interpretation software (for example, tracking reflections between manually-picked ``seed'' points), but often struggle when they encounter situations such as a discontinuous boundary, or one which varies in intensity. Such situations are extremely common in seismic data, especially along the boundary between salt bodies and other types of rock. Recent research has involved implementing the NCIS algorithm for the purpose of tracking these salt boundaries [e.g., Lomask et al. (2007); Lomask (2007); Halpert et al. (2009)]. Results of this line of research are encouraging; however, there are significant limitations, most notably computational. The NCIS algorithm calls for an edge weight matrix of size 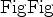 , where
, where 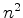 is the number of pixels in the image; this matrix quickly grows very large, especially for 3D surveys. Computationally, calculation of eigenvectors for such a large matrix is an extremely demanding task. As such, this method is limited to relatively small images; alternatively, we can restrict the computational domain to a specific region around a previously interpreted boundary. However, this means the method is of limited utility if there is no ``best guess'' model available, or if the accuracy of that model is in question.
is the number of pixels in the image; this matrix quickly grows very large, especially for 3D surveys. Computationally, calculation of eigenvectors for such a large matrix is an extremely demanding task. As such, this method is limited to relatively small images; alternatively, we can restrict the computational domain to a specific region around a previously interpreted boundary. However, this means the method is of limited utility if there is no ``best guess'' model available, or if the accuracy of that model is in question.
Thus, a more efficient global segmentation scheme that can include the entire image in the computational domain would be a very useful tool for interpretation of seismic images. One candidate for such a scheme is the algorithm from Felzenszwalb and Huttenlocher (2004), who write:
``Our algorithm is unique, in that it is both highly efficient and yet captures non-local properties of images.''
These two features are crucial for the task of seismic image segmentation. The algorithm is designed to run in
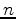 time, where
time, where 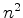 is the number of pixels in the graph; in contrast, other methods such as NCIS require closer to
is the number of pixels in the graph; in contrast, other methods such as NCIS require closer to 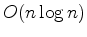 time to run. This represents a significant cost savings, especially for very large 3D seismic datasets that are becoming increasingly common.
time to run. This represents a significant cost savings, especially for very large 3D seismic datasets that are becoming increasingly common.
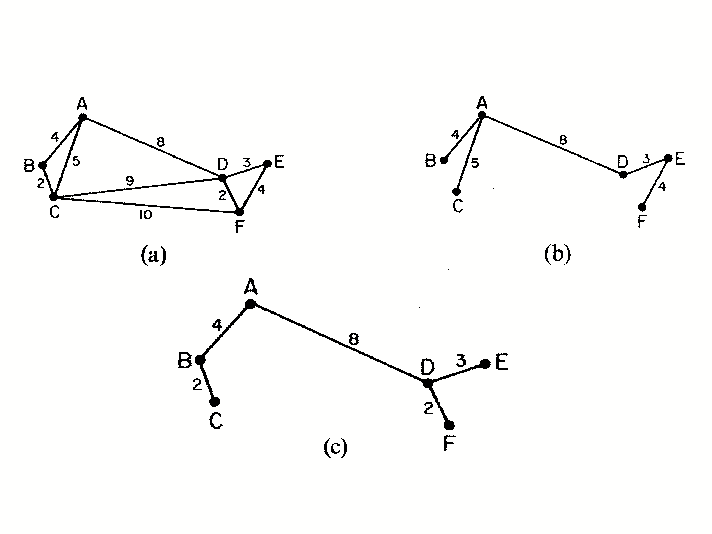
MST
Figure 2. Modified from Zahn (1971). A graph with weighted edges (a); a spanning tree of that graph (b); and the minimum spanning tree of the graph (c).
|
|
![[pdf]](icons/pdf.png) ![[png]](icons/viewmag.png)
|
|---|
The algorithm proposed by Felzenszwalb and Huttenlocher (2004) relies heavily on the concept of the ``Minimum Spanning Tree'' [see Zahn (1971)]. A graph's edges may be weighted using a measure of dissimilarity between vertex pairs; a connected graph is defined as one in which all such edges are assigned a weight value. If a spanning tree is a connected graph which connects all vertices of the graph without forming a circuit, the minimum spanning tree (MST) of a graph is the spanning tree with the minimum sum of edge weights (see Figure 2). In Zahn (1971), partitioning of a graph was achieved simply by cutting through edges with large weights. However, this approach is inadequate for images with coherent regions that are nonetheless highly heterogeneous (for example, consider the heterogeneous nature of the intensity values within the salt bodies in the examples above). However, the MST concept allows Felzenszwalb and Huttenlocher (2004) to develop what they term a ``pairwise region comparison" predicate. They define the internal difference of a region 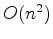 in the graph to be the largest edge weight of the MST of that region:
in the graph to be the largest edge weight of the MST of that region:
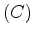 |
(1) |
where 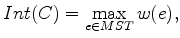 is a graph edge and
is a graph edge and 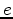 is the edge's weight, defined according to some simple algorithm. When comparing two regions (such as
is the edge's weight, defined according to some simple algorithm. When comparing two regions (such as 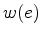 and
and 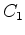 ), they define the minimum internal difference for the two regions to be
), they define the minimum internal difference for the two regions to be
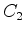 |
(2) |
where 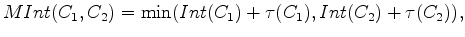 is a thresholding function that in a sense determines the scale at which the segmentation problem is approached, and thus indirectly the size of the regions in the final segmentation. Finally, they define the difference between the two regions to be the smallest edge weight that connects them:
is a thresholding function that in a sense determines the scale at which the segmentation problem is approached, and thus indirectly the size of the regions in the final segmentation. Finally, they define the difference between the two regions to be the smallest edge weight that connects them:
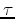 |
(3) |
where 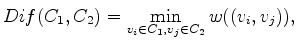 and
and 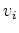 are vertices (or pixels) in the two different regions. When determining whether these two regions should be considered separate segments of the graph, or merged into a single region, they simply compare the values of
are vertices (or pixels) in the two different regions. When determining whether these two regions should be considered separate segments of the graph, or merged into a single region, they simply compare the values of
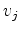 and
and
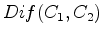 . If
. If
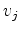 is greater, the ``pairwise comparison predicate'' is determined to be true, and the two regions are separated. While this is a relatively simple procedure, it is designed to allow highly heterogeneous regions to be segmented as a single component of an image. Additionally, Felzenszwalb and Huttenlocher (2004) note that their algorithm produces segmentations that are ``neither too coarse nor too fine," referring to the global capabilities of the segmentation process.
is greater, the ``pairwise comparison predicate'' is determined to be true, and the two regions are separated. While this is a relatively simple procedure, it is designed to allow highly heterogeneous regions to be segmented as a single component of an image. Additionally, Felzenszwalb and Huttenlocher (2004) note that their algorithm produces segmentations that are ``neither too coarse nor too fine," referring to the global capabilities of the segmentation process.
In the next section, I will provide more detail about the algorithm itself, and explain the modifications necessary to make it suitable for use with seismic images.
 |
 |
 |
 | A new method for more efficient seismic image segmentation |  |
![[pdf]](icons/pdf.png) |
Next: Approach
Up: Halpert: Faster image segmentation
Previous: Introduction
2010-05-19

![]() in the graph to be the largest edge weight of the MST of that region:
in the graph to be the largest edge weight of the MST of that region: