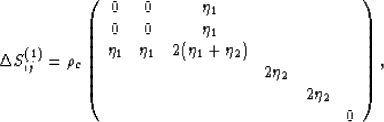
To illustrate the Sayers and Kachanov (1991) crack-influence parameter method, consider the situation in which all the cracks in the system have the same vertical (or z-)axis of symmetry. (We use 1,2,3 and x,y,z notation interchangeably for the axes.) Then, the cracked/fractured system is not isotropic, and we have the first-order compliance correction matrix for horizontal fractures, which is:
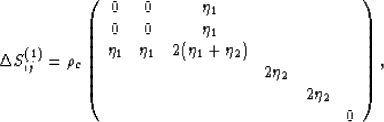 |
(9) |
Now it is also not difficult to see that, if the cracks were oriented
instead so that all their normals were pointed horizontally along the
x-axis, then we would have one permutation of this matrix and, if
instead they were all pointed horizontally along the y-axis, then we
would have a third permutation of the matrix. To obtain an
isotropic compliance correction matrix, we can simply average these three
permutations: just add the three ![]() 's together
and then divide by three. [Note that this method of averaging,
although correct for contributions linear in
's together
and then divide by three. [Note that this method of averaging,
although correct for contributions linear in ![]() , does not necessarily
work for higher order corrections (Berryman, 2007).]
This construction shows in part both the power and the simplicity of
the Sayers and Kachanov (1991) approach. The connection to the isotropic
case is of great practical importance, because it permits us to estimate the
parameters
, does not necessarily
work for higher order corrections (Berryman, 2007).]
This construction shows in part both the power and the simplicity of
the Sayers and Kachanov (1991) approach. The connection to the isotropic
case is of great practical importance, because it permits us to estimate the
parameters ![]() and
and ![]() by studying isotropic cracked/fractured
systems, using well-understood effective medium theories
(Zimmerman, 1991; Berryman and Grechka, 2006).
by studying isotropic cracked/fractured
systems, using well-understood effective medium theories
(Zimmerman, 1991; Berryman and Grechka, 2006).