




Next: Theoretical analysis of the
Up: Anisotropic parameter estimation from
Previous: RMO analysis in ADCIGs
Equation 5 shows that using usual notations, the estimation problem can be formulated as a
conventional inversion problem. For a given reflector at a given midpoint, we represent the
RMO values for different aperture angles by the data vector 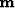 . We represent the
perturbation vector by the model vector
. We represent the
perturbation vector by the model vector 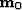 and denote
and denote 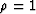 the vector of correct migration velocity
(
the vector of correct migration velocity
( ). The forward problem from equation 5 can thus be written
). The forward problem from equation 5 can thus be written
| 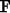 |
(6) |
Under linearization around the correct migration velocity, the estimation of the anisotropic
parameters is thus equivalent to a conventional inversion problem: it consists in inverting the
forward modeling matrix 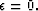 to estimate the anisotropic parameters
to estimate the anisotropic parameters 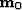 .
.





Next: Theoretical analysis of the
Up: Anisotropic parameter estimation from
Previous: RMO analysis in ADCIGs
Stanford Exploration Project
1/16/2007
 ). The forward problem from equation 5 can thus be written
). The forward problem from equation 5 can thus be written
![]() to estimate the anisotropic parameters
to estimate the anisotropic parameters ![]() .
.