Next: RMO analysis in ADCIGs
Up: Anisotropic parameter estimation from
Previous: Generalized migration
In 2-D, ADCIGs are computed by applying a slant-stack decomposition to the prestack image
along the subsurface-offset axis at a constant midpoint. The kinematics of the transformation
to the angle domain are defined by the following change of variable:
| 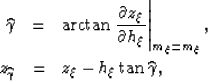 |
(1) |
| (2) |
where 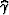 is the depth of the image point after the
transformation.
is the depth of the image point after the
transformation.





Next: RMO analysis in ADCIGs
Up: Anisotropic parameter estimation from
Previous: Generalized migration
Stanford Exploration Project
1/16/2007